
分析 方法一:將直線方程代入拋物線方程,利用韋達定理及拋物線的焦點弦公式,求得丨AB丨,根據拋物線的定義,即可求得丨AD丨+丨BC丨,則丨CD丨=丨BH丨=丨AB丨×sinα,即可求得四邊形ABCD的周長;
方法二:根據拋物線焦點弦的二級公式,丨AB丨=$\frac{2p}{si{n}^{2}α}$,根據拋物線的定義,即可求得丨AD丨+丨BC丨,則丨CD丨=丨BH丨=丨AB丨×sinα,即可求得四邊形ABCD的周長.
解答 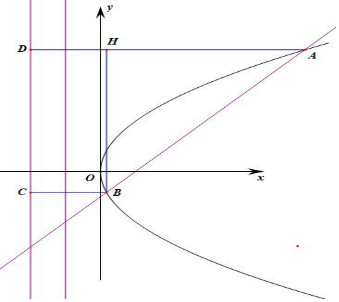 解:方法一:拋物線C:y2=4x的焦點是F(1,0),直線直線l1:y=x-1故拋物線的焦點,設A(x1,y1),B(x2,y2),
解:方法一:拋物線C:y2=4x的焦點是F(1,0),直線直線l1:y=x-1故拋物線的焦點,設A(x1,y1),B(x2,y2),
則$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=x-1}\end{array}\right.$,整理得:x2-6x+1=0,
x1+x2=6,
由丨AB丨=x1+x2+p=6+2+8,
由拋物線的定義可知:丨AD丨+丨BC丨=丨AB丨+2=10,
過B作BH⊥AD,
則由直線AB的傾斜角α=$\frac{π}{4}$,
則丨BH丨=丨AB丨×sinα=4$\sqrt{2}$,則丨CD丨=丨BH丨=4$\sqrt{2}$,
四邊形ABCD的周長丨AB丨+丨AD丨+丨BC丨+丨CD丨=18+4$\sqrt{2}$,
故答案為:18+4$\sqrt{2}$.
方法二:拋物線C:y2=4x的焦點是F(1,0),直線直線l1:y=x-1故拋物線的焦點,由直線AB的傾斜角α=$\frac{π}{4}$,
由丨AB丨=$\frac{2p}{si{n}^{2}α}$=$\frac{4}{(\frac{\sqrt{2}}{2})^{2}}$=8,
由拋物線的定義可知:丨AD丨+丨BC丨=丨AB丨+2=10,
則丨BH丨=丨AB丨×sinα=4$\sqrt{2}$,則丨CD丨=丨BH丨=4$\sqrt{2}$,
四邊形ABCD的周長丨AB丨+丨AD丨+丨BC丨+丨CD丨=18+4$\sqrt{2}$,
故答案為:18+4$\sqrt{2}$.
點評 本題考查直線與拋物線位置關系,考查拋物線的焦點弦公式,拋物線的定義,考查數形結合思想,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | -$\frac{{\sqrt{3}}}{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
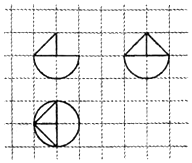
| A. | 3π+$\sqrt{3}$ | B. | 3π+$\sqrt{3}$+1 | C. | 5π+$\sqrt{3}$ | D. | 5π+$\sqrt{3}$+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
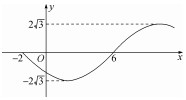 已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分圖象如圖所示,則函數g(x)=Acos(φx+ω)圖象的一個對稱中心可能為( )
已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分圖象如圖所示,則函數g(x)=Acos(φx+ω)圖象的一個對稱中心可能為( )| A. | $(-\frac{5}{2},0)$ | B. | $(\frac{1}{6},0)$ | C. | $(-\frac{1}{2},0)$ | D. | $(-\frac{11}{6},0)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com