已知b>-1,c>0,函數f(x)=x+b的圖象與函數g(x)=x2+bx+c的圖象相切.
(Ⅰ)求b與c的關系式(用c表示b);
(Ⅱ)設函數F(x)=f(x)g(x)在(-∞,+∞)內有極值點,求c的取值范圍.
【答案】
分析:(1)注意把握題目中的信息,f(x)和g(x)在同一點處具有相同的切線斜率.即f′(x
)=g′(x
)
(2)由構造的新函數F(x)在R上有極值點,得到二次函數F′(x)有兩個零點,再將上題的結論代入可解.
解答:解:(Ⅰ)依題意,令f'(x)=g'(x),得2x+b=1,
故
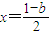
.由于

,得(b+1)
2=4c.
∵

,∴

.
(Ⅱ)F(x)=f(x)g(x)=x
3+2bx
2+(b
2+c)x+bc.
F′(x)=3x
2+4bx+b
2+c.
令F'(x)=0,即3x
2+4bx+b
2+c=0.
則△=16b
2-12(b
2+c)=4(b
2-3c).
若△=0,則F'(x)=0有一個實根x
,且F'(x)的變化如下:

于是x=x
不是函數F(x)的極值點.若△>0,
則F′(x)=0有兩個不相等的實根x
1,x
2(x
1<x
2)且F′(x)的變化如下:

由此,x=x
1是函數F(x)的極大值點,x=x
2是函數F(x)的極小值點.
綜上所述,當且僅當△=0時,函數F(x)在(-∞,+∞)上有極值點.

.
∵
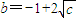
,∴

.
解之得0<c<7-4

或c>7+4
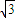
.
故所求c的取值范圍是(0,7-4
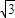
)∪(7+4

,+∞).
點評:本題考查導數、切線、極值等知識及綜合運用數學知識解決問題的能力.其中三次多項式函數也是高考中對導數考查的常見載體.

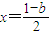 .由于
.由于 ,得(b+1)2=4c.
,得(b+1)2=4c. ,∴
,∴ .
.

 .
.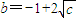 ,∴
,∴ .
. 或c>7+4
或c>7+4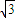 .
.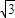 )∪(7+4
)∪(7+4 ,+∞).
,+∞).
