
【題目】已知![]() 命題p:對任意
命題p:對任意![]() ,不等式
,不等式![]() 恒成立;命題q:存在
恒成立;命題q:存在![]() ,使得
,使得![]() 成立.
成立.
(1)若p為真命題,求m的取值范圍;
(2)當![]() ,若p且q為假,p或q為真,求m的取值范圍.
,若p且q為假,p或q為真,求m的取值范圍.
【答案】(1) [1,2].(2) (-∞,1)∪(1,2].
【解析】試題分析:(1)(2x-2)min≥m2-3m.即m2-3m≤-2,解得1≤m≤2;(2)p,q中一個是真命題,一個是假命題,解得m的取值范圍為(-∞,1)∪ (1,2].
試題解析:
(1)∵對任意x∈[0,1],不等式2x-2≥m2-3m恒成立,
∴(2x-2)min≥m2-3m.即m2-3m≤-2.
解得1≤m≤2.
因此,若p為真命題時,m的取值范圍是[1,2].
(2)∵a=1,且存在x∈[-1,1],使得m≤ax成立,
∴m≤x,命題q為真時,m≤1.
∵p且q為假,p或q為真,
∴p,q中一個是真命題,一個是假命題.
當p真q假時,則![]() 解得1<m≤2;
解得1<m≤2;
當p假q真時,![]() 即m<1.
即m<1.
綜上所述,m的取值范圍為(-∞,1)∪(1,2].


 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:
【題目】已知點![]() 為圓
為圓![]() 的圓心,
的圓心, ![]() 是圓上動點,點
是圓上動點,點![]() 在圓的半徑
在圓的半徑![]() 上,且有點
上,且有點![]() 和
和![]() 上的點
上的點![]() ,滿足
,滿足![]()
(1)當![]() 在圓上運動時,求點
在圓上運動時,求點![]() 的軌跡方程;
的軌跡方程;
(2)若斜率為![]() 的直線
的直線![]() 與圓
與圓![]() 相切,與(1)中所求點
相切,與(1)中所求點![]() 的軌跡教育不同的兩點
的軌跡教育不同的兩點![]()
![]() 是坐標原點,且
是坐標原點,且![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2015年12月,華中地區數城市空氣污染指數“爆表”,此輪污染為2015年以來最嚴重的污染過程,為了探究車流量與![]() 的濃度是否相關,現采集到華中某城市2015年12月份某星期星期一到星期日某一時間段車流量與
的濃度是否相關,現采集到華中某城市2015年12月份某星期星期一到星期日某一時間段車流量與![]() 的數據如表:
的數據如表:

(1)由散點圖知![]() 與
與![]() 具有線性相關關系,求
具有線性相關關系,求![]() 關于
關于![]() 的線性回歸方程;(提示數據:
的線性回歸方程;(提示數據: ![]() )
)
(2)利用(1)所求的回歸方程,預測該市車流量為12萬輛時![]() 的濃度.
的濃度.
參考公式:回歸直線的方程是![]() ,其中
,其中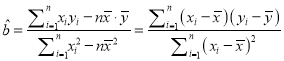 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一裝有水的直三棱柱ABC-A1B1C1容器(厚度忽略不計),上下底面均為邊長為5的正三角形,側棱為10,側面AA1B1B水平放置,如圖所示,點D、E、F、G分別在棱CA、CB、C1B1、C1A1上,水面恰好過點D,E,F,C,且CD=2

(1)證明:DE∥AB;
(Ⅱ)若底面ABC水平放置時,求水面的高
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廣場有一塊不規則的綠地如圖所示,城建部門欲在該地上建造一個底座為三角形的環境標志,小李,小王設計的底座形狀分別為![]() ,
, ![]() ,經測量
,經測量![]() 米,
米, ![]() 米,
米, ![]() 米,
米, ![]()
(I)求![]() 的長度;
的長度;
(Ⅱ)若環境標志的底座每平方米造價為![]() 元,不考慮其他因素,小李,小王誰的設計建造費用最低(請說明理由),最低造價為多少?(
元,不考慮其他因素,小李,小王誰的設計建造費用最低(請說明理由),最低造價為多少?(![]() )
)

查看答案和解析>>
科目:高中數學 來源: 題型:
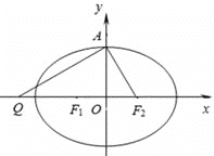
【題目】設橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,上頂點為A,過點A與
,上頂點為A,過點A與![]() 垂直的直線交
垂直的直線交![]() 軸負半軸于點
軸負半軸于點![]() ,且
,且![]() ,若過
,若過![]() ,
, ![]() ,
, ![]() 三點的圓恰好與直線
三點的圓恰好與直線![]() 相切.過定點
相切.過定點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點(點
兩點(點![]() 在點
在點![]() ,
, ![]() 之間).
之間).
(Ⅰ)求橢圓![]() 的方程;(Ⅱ)若實數
的方程;(Ⅱ)若實數![]() 滿足
滿足![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() ,
, ![]() ,且滿足
,且滿足![]() .
.
(1)求點![]() 的軌跡方程所代表的曲線
的軌跡方程所代表的曲線![]() ;
;
(2)若點![]() ,
, ![]() ,
, ![]() 是曲線
是曲線![]() 上的動點,點
上的動點,點![]() 在直線
在直線![]() 上,且滿足
上,且滿足![]() ,
, ![]() ,當點
,當點![]() 在
在![]() 上運動時,求點
上運動時,求點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,以原點為圓心,橢圓的短半軸長為半徑的圓與直線
,以原點為圓心,橢圓的短半軸長為半徑的圓與直線![]() 相切.
相切. ![]() 、
、![]() 是橢圓
是橢圓![]() 的右頂點與上頂點,直線
的右頂點與上頂點,直線![]() 與橢圓相交于
與橢圓相交于![]() 、
、![]() 兩點.
兩點.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)當四邊形![]() 面積取最大值時,求
面積取最大值時,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com