
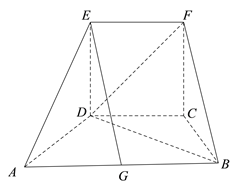
【題目】如圖所示的幾何體中,四邊形![]() 為等腰梯形,
為等腰梯形, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,四邊形
,四邊形![]() 為正方形,平面
為正方形,平面![]() 平面
平面![]() .
.
(Ⅰ)若點![]() 是棱
是棱![]() 的中點,求證:
的中點,求證: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】(1)見解析(2)![]() (3)見解析
(3)見解析
【解析】試題分析: (1)由![]() //
// ![]() ,且
,且![]() ,故四邊形
,故四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() //
// ![]() .所以
.所以![]() //平面
//平面![]() ; (2)因為平面
; (2)因為平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() . 在△
. 在△![]() 中,由余弦定理,得
中,由余弦定理,得![]() ,所以
,所以![]() , 如圖,以
, 如圖,以![]() 為原點,以
為原點,以![]() 所在直線分別為
所在直線分別為![]() 軸,建立空間坐標系,寫出各點坐標,求出平面的法向量,根據線面角公式求值即可; (3)假設線段
軸,建立空間坐標系,寫出各點坐標,求出平面的法向量,根據線面角公式求值即可; (3)假設線段![]() 上存在點
上存在點![]() ,設
,設 ,分別求出兩個平面的法向量,令數量積為0,方程無解,故不存在.
,分別求出兩個平面的法向量,令數量積為0,方程無解,故不存在.
試題解析:(Ⅰ)證明:由已知得![]() //
// ![]() ,且
,且![]() .
.
因為![]() 為等腰梯形,所以有
為等腰梯形,所以有![]() //
// ![]() .
.
因為![]() 是棱
是棱![]() 的中點,所以
的中點,所以![]() .
.
所以![]() //
// ![]() ,且
,且![]() ,
,
故四邊形![]() 為平行四邊形,
為平行四邊形,
所以![]() //
// ![]() .
.
因為![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]() .
.
解: (Ⅱ)因為四邊形
(Ⅱ)因為四邊形![]() 為正方形,所以
為正方形,所以![]() .
.
因為平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
在△![]() 中,因為
中,因為![]() ,
, ![]() ,
,
所以由余弦定理,得![]() ,
,
所以![]() .
.
在等腰梯形![]() 中,可得
中,可得![]() .
.
如圖,以![]() 為原點,以
為原點,以![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,
建立空間坐標系,
則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,  ,
,
所以![]() ,
,  ,
, ![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,由
,由
所以 ,取
,取![]() ,則
,則![]() ,得
,得![]() .
.
設直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
則 ,
,
![]()
所以![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() .
.
(Ⅲ)線段![]() 上不存在點
上不存在點![]() ,使平面
,使平面![]()
![]() 平面
平面![]() .證明如下:
.證明如下:
假設線段![]() 上存在點
上存在點![]() ,設
,設 ,
,
則 .
.
設平面![]() 的法向量為
的法向量為![]() ,由
,由
所以 ,
,
取![]() ,則
,則![]() ,得
,得![]() .
.
要使平面 平面
平面![]() ,只需
,只需![]() ,
,
即![]() , 此方程無解.
, 此方程無解.
所以線段![]() 上不存在點
上不存在點![]() ,使平面
,使平面![]()
![]() 平面
平面![]() .
.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:高中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列4個結論①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;
其中正確的結論是 . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x|x|+bx+c(b,c∈R),給出如下四個命題:①若c=0,則f(x)為奇函數;②若b=0,則函數f(x)在R上是增函數;③函數y=f(x)的圖象關于點(0,c)成中心對稱圖形;④關于x的方程f(x)=0最多有兩個實根.其中正確的命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若無窮數列![]() 滿足:
滿足: ![]() ,對于
,對于![]() ,都有
,都有![]() (其中
(其中![]() 為常數),則稱
為常數),則稱![]() 具有性質“
具有性質“![]() ”.
”.
(Ⅰ)若![]() 具有性質“
具有性質“![]() ”,且
”,且![]() ,
, ![]() ,
, ![]() ,求
,求![]() ;
;
(Ⅱ)若無窮數列![]() 是等差數列,無窮數列
是等差數列,無窮數列![]() 是公比為正數的等比數列,
是公比為正數的等比數列, ![]() ,
, ![]() ,
, ![]() ,判斷
,判斷![]() 是否具有性質“
是否具有性質“![]() ”,并說明理由;
”,并說明理由;
(Ⅲ)設![]() 既具有性質“
既具有性質“![]() ”,又具有性質“
”,又具有性質“![]() ”,其中
”,其中![]() ,
, ![]() ,
, ![]() 互質,求證:
互質,求證: ![]() 具有性質“
具有性質“![]() ”.
”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】奇函數f(x)、偶函數g(x)的圖象分別如圖1、2所示,方程f(g(x))=0、g(f(x))=0的實根個數分別為a、b,則a+b=( ) 
A.14
B.10
C.7
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“城中觀海”是近年來國內很多大中型城市內澇所致的現象,究其原因,除天氣因素、城市規劃等原因外,城市垃圾雜物也是造成內澇的一個重要原因.暴雨會沖刷城市的垃圾雜物一起進入下水道,據統計,在不考慮其它因素的條件下,某段下水道的排水量V(單位:立方米/小時)是雜物垃圾密度x(單位:千克/立方米)的函數.當下水道的垃圾雜物密度達到2千克/立方米時,會造成堵塞,此時排水量為0;當垃圾雜物密度不超過0.2千克/立方米時,排水量是90立方米/小時;研究表明,0.2≤x≤2時,排水量V是垃圾雜物密度x的一次函數.
(1)當0≤x≤2時,求函數V(x)的表達式;
(2)當垃圾雜物密度x為多大時,垃圾雜物量(單位時間內通過某段下水道的垃圾雜物量,單位:千克/小時)f(x)=xV(x)可以達到最大,求出這個最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四名同學根據各自的樣本數據研究變量![]() 之間的相關關系,并求得回歸直線方程,分別得到以下四個結論:( )
之間的相關關系,并求得回歸直線方程,分別得到以下四個結論:( )
①![]() 與
與![]() 負相關且
負相關且![]() . ②
. ②![]() 與
與![]() 負相關且
負相關且![]()
③![]() 與
與![]() 正相關且
正相關且![]() ④
④![]() 與
與![]() 正相關且
正相關且![]()
其中正確的結論的序號是( )
A. ①② B. ②③ C. ①④ D. ③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高級中學共有學生2000名,各年級男、女生人數如表:

已知在全校學生中隨機抽取1名,抽到高二年級女生的概率是0.19.
(1)求![]() 的值;
的值;
(2)現用分層抽樣的方法在全校抽取48名學生,問應該在高三年級抽取多少名?
(3)已知![]() ,求高三年級中女生比男生多的概率.
,求高三年級中女生比男生多的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com