【題目】某高級中學共有學生2000名，各年級男、女生人數如表：
已知在全校學生中隨機抽取1名，抽到高二年級女生的概率是0.19.
（1）求
的值；
（2）現用分層抽樣的方法在全校抽取48名學生，問應該在高三年級抽取多少名？
（3）已知
，求高三年級中女生比男生多的概率.
【答案】（1）
；（2）
；（3）
.
【解析】試題分析：（1）用頻率估計概率，可將概率是0.19看作是頻率，求出高二女生的人數，可求出x值，
（2）再用全校的人數減去高一和高二的人數，得到高三的人數，全校要抽取48人，做出每個個體被抽到的概率，做出高三被抽到的人數．
（3）設出高三年級女生比男生多的事件為A，高三年級女生，男生數記為（y，z），因為y+z=500，且y，z∈N，列舉出基本事件空間包含的基本事件有共11個，事件A包含的基本事件數，得到結果．
試題解析：
（1）∵
，∴
.
（2） 高三年級人數為： 
，
現用分層抽樣的方法在全校抽取48名學生，應在高三年級抽取的人數為： 
人.
（3）設高三年級女生比男生多的事件為
，高三年級女生男生數記為
，
由（2）
且
，基本事件空間包含的基本事件有： 
共11個，
事件
包含的基本事件有： 
，共5個，
∴
.
新課標同步訓練系列答案
一線名師口算應用題天天練一本全系列答案科目：高中數學 來源： 題型：
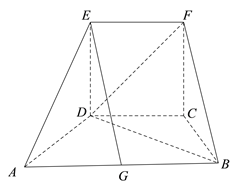
【題目】如圖所示的幾何體中，四邊形
為等腰梯形， 
∥
， 
， 
，四邊形
為正方形，平面
平面
.
（Ⅰ）若點
是棱
的中點，求證： 
∥平面
；
（Ⅱ）求直線
與平面
所成角的正弦值；
（Ⅲ）在線段
上是否存在點
，使平面
平面
？若存在，求
的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設偶函數f（x）滿足f（x）=x3﹣8（x≥0），則{x|f（x﹣2）＞0}=（ ）
A.{x|x＜﹣2或x＞4}
B.{x|x＜0或x＞4}
C.{x|x＜0或x＞6}
D.{x|x＜﹣2或x＞2}
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知坐標平面上點
與兩個定點
， 
的距離之比等于5.
（1）求點
的軌跡方程，并說明軌跡是什么圖形；
（2）記（1）中的軌跡為
，過點
的直線
被
所截得的線段的長為 8，求直線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）=x2﹣ax+3，且對任意的實數x都有f（4﹣x）=f（x）成立．
（1）求實數a的值；
（2）求函數f（x）在區間[0，3]上的值域；
（3）要得到函數y=x2的圖象只需要將二次函數y=f（x）的圖象做怎樣的變換得到．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合A={x| 
＞0}，集合B={x|y=lg（﹣x2+3x+28）}，集合C={x|m+1≤x≤2m﹣1}．
（1）求（RA）∩B；
（2）若B∪C=B，求實數m的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
