
【題目】已知函數(shù)![]() ,
,![]() ,其中
,其中![]() 為常數(shù),函數(shù)
為常數(shù),函數(shù)![]() 和
和![]() 的圖象在它們與坐標(biāo)軸交點處的切線互相平行.
的圖象在它們與坐標(biāo)軸交點處的切線互相平行.
(1)求![]() 的值;
的值;
(2)若存在![]() ,使不等式
,使不等式![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)令![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】
(1)分別求出![]() 與
與![]() 與y軸和x軸的交點坐標(biāo),求出兩函數(shù)在與坐標(biāo)軸交點處的導(dǎo)數(shù),由導(dǎo)數(shù)值相等求得a的值;
與y軸和x軸的交點坐標(biāo),求出兩函數(shù)在與坐標(biāo)軸交點處的導(dǎo)數(shù),由導(dǎo)數(shù)值相等求得a的值;
(2)由(1)中求得的a值得到![]() 的解析式,代入
的解析式,代入![]() ,把存在
,把存在![]() 使不等式恒成立轉(zhuǎn)化為存在
使不等式恒成立轉(zhuǎn)化為存在![]() ,不等式
,不等式![]() 恒成立,構(gòu)造函數(shù)
恒成立,構(gòu)造函數(shù)![]() ,
,![]() ,利用導(dǎo)數(shù)求其最大值后得答案;
,利用導(dǎo)數(shù)求其最大值后得答案;
(3)把![]() ,
,![]() 代入
代入![]() ,去絕對值后得到
,去絕對值后得到![]() (
(![]() ),借助于兩個輔助函數(shù)
),借助于兩個輔助函數(shù)![]() (
(![]() ),
),![]() (
(![]() ),證得
),證得![]() ,
,![]() ,兩式聯(lián)立后得答案.
,兩式聯(lián)立后得答案.
(1)![]() 的圖象與
的圖象與![]() 軸的交點為
軸的交點為![]() ,
,![]() 的圖象與
的圖象與![]() 軸的交點為
軸的交點為![]() ,
,
![]() ,
,![]() (
(![]() ),由
),由![]() ,
,![]() ,得
,得![]() ;
;
(2)因為![]() ,令
,令![]() ,
,![]() ,
,
則![]() ,
,
所以![]() 在
在![]() 上是減函數(shù),所以
上是減函數(shù),所以![]() ,
,
因為“存在![]() ,使不等式
,使不等式![]() 成立”的充要條件是
成立”的充要條件是![]() ,
,
所以![]() 的取值范圍為
的取值范圍為![]() ;
;
(3)![]() (
(![]() ),
),
記![]() (
(![]() ),因為
),因為![]() ,所以
,所以![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
又因為![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,①
,①
記![]() (
(![]() ),因為
),因為![]() ,所以
,所以![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù),
上是減函數(shù),
所以![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,②
,②
由①②可得![]() ,所以
,所以![]() ,即
,即![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】半正多面體亦稱“阿基米德多面體”,是由邊數(shù)不全相同的正多邊形為面組成的多面體.如將正四面體所有棱各三等分,沿三等分點從原幾何體割去四個小正四面體如圖所示,余下的多面體就成為一個半正多面體,若這個半正多面體的棱長為2,則這個半正多面體的體積為______.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在悠久燦爛的中國古代文化中,數(shù)學(xué)文化是其中的一朵絢麗的奇葩.《張丘建算經(jīng)》是我國古代有標(biāo)志性的內(nèi)容豐富的眾多數(shù)學(xué)名著之一,大約創(chuàng)作于公元五世紀.書中有如下問題:“今有女善織,日益功疾,初日織五尺,今一月織九匹三丈,問日益幾何?”.其大意為:“有一女子擅長織布,織布的速度一天比一天快,從第二天起,每天比前一天多織相同數(shù)量的布,第一天織![]() 尺,一個月共織了九匹三丈,問從第二天起,每天比前一天多織多少尺布?”.已知
尺,一個月共織了九匹三丈,問從第二天起,每天比前一天多織多少尺布?”.已知![]() 匹
匹![]() 丈,
丈,![]() 丈
丈![]() 尺,若這一個月有
尺,若這一個月有![]() 天,記該女子這一個月中的第
天,記該女子這一個月中的第![]() 天所織布的尺數(shù)為
天所織布的尺數(shù)為![]() ,
,![]() ,對于數(shù)列
,對于數(shù)列![]() 、
、![]() ,下列選項中正確的為( )
,下列選項中正確的為( )
A.![]() B.
B.![]() 是等比數(shù)列C.
是等比數(shù)列C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,焦距為
,焦距為![]() .斜率為
.斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 有兩個不同的交點
有兩個不同的交點![]() ,
,![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() .若
.若![]() ,
,![]() 和點
和點![]() 共線,求
共線,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】端午節(jié)是我國民間為紀念愛國詩人屈原的一個傳統(tǒng)節(jié)日.某市為了解端午節(jié)期間粽子的銷售情況,隨機問卷調(diào)查了該市1000名消費者在去年端午節(jié)期間的粽子購買量(單位:克),所得數(shù)據(jù)如下表所示:
購買量 |
|
|
|
|
|
人數(shù) | 100 | 300 | 400 | 150 | 50 |
將煩率視為概率
(1)試求消費者粽子購買量不低于300克的概率;
(2)若該市有100萬名消費者,請估計該市今年在端午節(jié)期間應(yīng)準(zhǔn)備多少千克棕子才能滿足市場需求(以各區(qū)間中點值作為該區(qū)間的購買量).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在一次數(shù)學(xué)考試中,從甲,乙兩個班級各抽取10名同學(xué)的成績進行統(tǒng)計分析,他們成績的莖葉圖如圖所示,成績不小于90分為及格.

(1)從兩班10名同學(xué)中各抽取一人,在有人及格的情況下,求乙班同學(xué)不及格的概率;
(2)從甲班10人中取一人,乙班10人中取兩人,三人中及格人數(shù)記為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
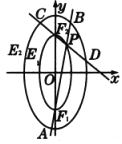
【題目】如圖對稱軸為坐標(biāo)軸,焦點均在![]() 軸上的兩橢圓
軸上的兩橢圓![]() ,
,![]() 的離心率相同且均為
的離心率相同且均為![]() ,橢圓
,橢圓![]() 過點
過點![]() 且其上頂點恰為橢圓
且其上頂點恰為橢圓![]() 的上焦點.
的上焦點.![]() 是橢圓
是橢圓![]() 上異于
上異于![]() ,
,![]() 的任意一點,直線
的任意一點,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,直線
兩點,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)求橢圓![]() ,
,![]() 的標(biāo)準(zhǔn)方程.
的標(biāo)準(zhǔn)方程.
(2)證明:![]() .
.
(3)![]() 是否為定值?若為定值.則求出該定值;否則,說明理由.
是否為定值?若為定值.則求出該定值;否則,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)求![]() 時,函數(shù)
時,函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 有兩個零點,求正整數(shù)
有兩個零點,求正整數(shù)![]() 的最小值
的最小值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 定義在區(qū)間
定義在區(qū)間![]() 上,
上,![]() ,且當(dāng)
,且當(dāng)![]() 時,恒有
時,恒有![]() ,又數(shù)列
,又數(shù)列![]() 滿足
滿足![]() ,
,![]() ,設(shè)
,設(shè)![]() ,對于任意的
,對于任意的![]() ,
,![]() 的最小自然數(shù)
的最小自然數(shù)![]() 的值為_______________________________.
的值為_______________________________.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com