
分析 直線l:x=my+b,代入拋物線方程可化為y2-2my-2b=0,y1y2=-2b,結合k1k2=$\frac{2}{3}$,即可得出結論.
解答 解:設A(x1,y1),B(x2,y2),k1k2=$\frac{2}{3}$,則$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{2}}{{x}_{2}}$=$\frac{2}{3}$,又y12=2x1,y22=2x2,
∴y1y2=6
直線l:x=my+b,代入拋物線方程可化為y2-2my-2b=0,
∴y1y2=-2b,
∴-2b=6,∴b=-3,
即直線l:x=my-3,
∴l一定過點(-3,0),
故答案為:(-3,0).
點評 本題考查拋物線方程,考查直線與拋物線的位置關系,比較基礎.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
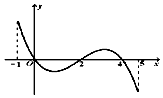 已知函數f(x)的定義域為[-1,5],部分對應值如下表,
已知函數f(x)的定義域為[-1,5],部分對應值如下表,| x | -1 | 0 | 4 | 5 |
| f(x) | -1 | 2 | 2 | -1 |
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
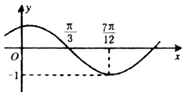 若f(x)=Asin(ωx+ϕ)(其中A>0,|φ|$<\frac{π}{2}$)的圖象如圖,為了得到$g(x)=sin(2x-\frac{π}{3})$的圖象,則需將f(x)的圖象( )
若f(x)=Asin(ωx+ϕ)(其中A>0,|φ|$<\frac{π}{2}$)的圖象如圖,為了得到$g(x)=sin(2x-\frac{π}{3})$的圖象,則需將f(x)的圖象( )| A. | 向右平移$\frac{π}{6}$個單位 | B. | 向右平移$\frac{π}{3}$個單位 | ||
| C. | 向左平移$\frac{π}{6}$個單位 | D. | 向左平移$\frac{π}{3}$個單位 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|1≤x<2} | B. | {x|1<x<2} | C. | {x|x<2} | D. | {x|x≥1} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
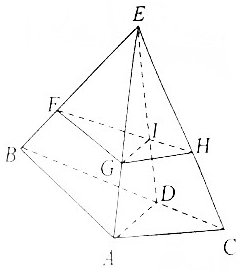 在三棱錐E-ABC中,AB⊥AC,AB=1,AC=$\frac{\sqrt{2}}{2}$,點D在線段BC上,且BD=2CD,ED⊥平面ABC,F,G,H是EB,EA,EC上的點,FH與ED交于點I.
在三棱錐E-ABC中,AB⊥AC,AB=1,AC=$\frac{\sqrt{2}}{2}$,點D在線段BC上,且BD=2CD,ED⊥平面ABC,F,G,H是EB,EA,EC上的點,FH與ED交于點I.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com