
【題目】過橢圓![]() 上一點
上一點![]() 作兩條直線
作兩條直線![]() ,
,![]() 與橢圓另交于
與橢圓另交于![]() ,
,![]() 點,設它們的斜率分別為
點,設它們的斜率分別為![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的面積
的面積![]() ;
;
(2)若![]() ,
,![]() ,求直線
,求直線![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1) 先通過點斜式分別寫出直線![]() ,
,![]() 的方程,再通過曲直聯立求出點
的方程,再通過曲直聯立求出點![]() 和
和![]() 的坐標,
的坐標,
從而求得直線![]() 的方程以及線段
的方程以及線段![]() 的長,然后利用點到直線的距離公式求出
的長,然后利用點到直線的距離公式求出![]() 的高,從而求得其面積.
的高,從而求得其面積.
(2)設![]() 的中點為
的中點為![]() 點,然后分類討論,①當直線
點,然后分類討論,①當直線![]() 過原點時,可得知直線
過原點時,可得知直線![]() 的方程為
的方程為![]() ;②當直線
;②當直線![]() 不過原點時,結合平面幾何知識可得點
不過原點時,結合平面幾何知識可得點![]() ,
,![]() ,
,![]() 三點共線,然后設直線
三點共線,然后設直線![]() 的方程為
的方程為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,再通過曲直聯立、韋達定理和點坐標公式,得到
,再通過曲直聯立、韋達定理和點坐標公式,得到![]() ,
,![]() ,所以直線
,所以直線![]() 斜率為
斜率為![]() ,所以直線
,所以直線![]() 的斜率與直線
的斜率與直線![]() 斜率不相等,即點
斜率不相等,即點![]() ,
,![]() ,
,![]() 三點不共線,與前面的結論矛盾,最后得到直線
三點不共線,與前面的結論矛盾,最后得到直線![]() 的方程為
的方程為![]() .
.
解:(1)因為![]() ,
,![]() ,
,
所以直線![]() ,
,![]() 方程分別為
方程分別為![]() ,
,![]() ,
,
由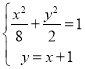 ,得:
,得:![]() ,
,
由此解得![]() ,
,![]() ,所以
,所以![]() ,
,
同理可得:![]() ,
,
所以直線![]() 的方程為
的方程為![]() ,
,
所以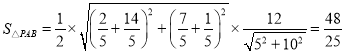 ,
,
(2)設![]() 的中點為
的中點為![]() 點,
點,
①當直線![]() 過原點時,點
過原點時,點![]() 與點
與點![]() 重合,
重合,
因為![]() ,所以
,所以![]() ,
,
所以直線![]() 的方程為
的方程為![]() ,
,
②當直線![]() 不過原點時.設
不過原點時.設![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在![]() 中,因為
中,因為![]() ,所以
,所以![]() ,
,
在![]() 中,因為
中,因為![]() ,所以
,所以![]() ,
,
所以點![]() ,
,![]() ,
,![]() 三點共線,
三點共線,
因為直線![]() 的斜率為
的斜率為![]() ,所以直線
,所以直線![]() 的斜率為
的斜率為![]() ,
,
設直線![]() 的方程為
的方程為![]() ,
,
由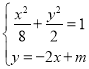 ,得:
,得:![]() ,
,
由韋達定理知,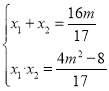 ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以直線![]() 斜率為
斜率為![]() ,所以直線
,所以直線![]() 的斜率與直線
的斜率與直線![]() 斜率不相等,
斜率不相等,
點![]() ,
,![]() ,
,![]() 三點不共線(與上面的結論矛盾),
三點不共線(與上面的結論矛盾),
綜上:所求直線![]() 的方程為
的方程為![]() .
.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,
,![]() ,上頂點為
,上頂點為![]() ,右焦點為
,右焦點為![]() ,已知
,已知![]() .
.
(1)證明:![]() .
.
(2)已知直線![]() 的傾斜角為
的傾斜角為![]() ,設
,設![]() 為橢圓
為橢圓![]() 上不同于
上不同于![]() ,
,![]() 的一點,
的一點,![]() 為坐標原點,線段
為坐標原點,線段![]() 的垂直平分線交
的垂直平分線交![]() 于
于![]() 點,過
點,過![]() 且垂直于
且垂直于![]() 的直線交
的直線交![]() 軸于
軸于![]() 點,若
點,若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】世界互聯網大會是由中國倡導并每年在浙江省嘉興市桐鄉烏鎮舉辦的世界性互聯網盛會,大會旨在搭建中國與世界互聯互通的國際平臺和國際互聯網共享共治的中國平臺,讓各國在爭議中求共識在共識中謀合作在合作中創共贏.2019年10月20日至22日,第六屆世界互聯網大會如期舉行,為了大會順利召開,組委會特招募了1 000名志愿者.某部門為了了解志愿者的基本情況,調查了其中100名志愿者的年齡,得到了他們年齡的中位數為34歲,年齡在![]() 歲內的人數為15,并根據調查結果畫出如圖所示的頻率分布直方圖:
歲內的人數為15,并根據調查結果畫出如圖所示的頻率分布直方圖:

(1)求![]() ,
,![]() 的值并估算出志愿者的平均年齡(同一組的數據用該組區間的中點值代表);
的值并估算出志愿者的平均年齡(同一組的數據用該組區間的中點值代表);
(2)這次大會志愿者主要通過現場報名和登錄大會官網報名,即現場和網絡兩種方式報名調查.這100位志愿者的報名方式部分數據如下表所示,完善下面的表格,通過計算說明能
否在犯錯誤的概率不超過0.001的前提下,認為“選擇哪種報名方式與性別有關系”?
男性 | 女性 | 總計 | |
現場報名 | 50 | ||
網絡報名 | 31 | ||
總計 | 50 |
參考公式及數據: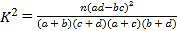 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,以坐標原點
為參數,以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,取相同長度單位建立極坐標系,曲線
軸的正半軸為極軸,取相同長度單位建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的普通方程;
的普通方程;
(2)設射線![]() 與曲線
與曲線![]() 交于不同于極點的點
交于不同于極點的點![]() ,與曲線
,與曲線![]() 交于不同于極點的點
交于不同于極點的點![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“沉魚、落雁、閉月、羞花”是由精彩故事組成的歷史典故.“沉魚”,講的是西施浣紗的故事;“落雁”,指的就是昭君出塞的故事;“閉月”,是述說貂蟬拜月的故事;“羞花”,談的是楊貴妃醉酒觀花時的故事.她們分別是中國古代的四大美女.某藝術團要以四大美女為主題排演一部舞蹈劇,已知乙扮演楊貴妃,甲、丙、丁三人抽簽決定扮演的對象,則甲不扮演貂蟬且丙扮演昭君的概率為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2014年,中央和國務院辦公廳印發《關于引導農村土地經營權有序流轉發展農業適度規模經營的意見》,要求大力發展土地流轉和適度規模經營.某種糧大戶2015年開始承包了一地區的大規模水田種植水稻,購買了一種水稻收割機若干臺,這種水稻收割機隨著使用年限的增加,每年的養護費也相應增加,這批水稻收割機自購買使用之日起,5年以來平均每臺水稻收割機的養護費用數據統計如下:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代碼 | 1 | 2 | 3 | 4 | 5 |
養護費用 | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
(1)從這5年中隨機抽取2年,求平均每臺水稻收割機每年的養護費用至少有1年多于2萬元的概率;
(2)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(3)若該水稻收割機的購買價格是每臺16萬元,由(2)中的回歸方程,從每臺水稻收割機的年平均費用角度,你認為一臺該水稻收割機是使用滿5年就淘汰,還是繼續使用到滿8年再淘汰?
附:回歸直線的斜率和截距的最小二乘法估計公式分別為: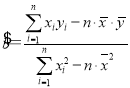 ,
,![]()
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com