【題目】如圖，在直三棱柱
中， 
是線段
上一點.
點.
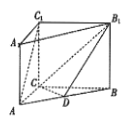
（1）確定
的位置，使得平面
平面
；
（2）若
平面
,設二面角
的大小為
，求證： 
【答案】（1）見解析（2）
【解析】試題分析：（1）當
時，可證明
平面
，再根據平面幾何知識求解即可；（2）以
、
、
所在直線分別為
軸、
軸、
軸建立如圖所示的空間直角坐標系，求出平面
的一個法向量及平面
的一個法向量，利用空間向量夾角余弦公式可得結果.
試題解析：（1）當
時，∵
，∴由射影定理得
，∴
.
∵
平面
，∴
.
∵
，∴
平面
.
又
平面
，∴當
時，平面
平面
.
（2）以
、
、
所在直線分別為
軸、
軸、
軸建立如圖所示的空間直角坐標系，
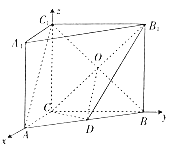
則
， 
， 
.
連接
交
于點
，則
為
的中點.
∵平面
平面
，且
平面
，∴
，∴
為
的中點.
∴
， 
，
設平面
的法向量為
，
則
，且
，
令
，可取平面
的一個法向量
，
而平面
的一個法向量為
，
∴
，∵二面角
為銳角，
∴
，又
，∴
.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】如圖，我海監船在
島海域例行維權巡航，某時刻航行至
處，此時測得其東北方向與它相距32海里的
處有一外國船只，且
島位于海監船正東
海里處．
（1）求此時該外國船只與
島的距離；
（2）觀測中發現，此外國船只正以每小時8海里的速度沿正南方向航行，為了將該船攔截在離
島24海里處，不讓其進入
島24海里內的海域，試確定海監船的航向，并求其速度的最小值．（參考數據： 
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以下莖葉圖記錄了甲，乙兩組各四名同學的植樹棵數.乙組記錄中有一個數據模糊，無法確認，在圖中以
表示.
（1）如果
，求乙組同學植樹棵數的平均數和方差；
（2）如果
，分別從甲，乙兩組中隨機選取一名同學，求這兩名同學的植樹總棵數為19的概率.（注：方差
，其中
為
， 
，……， 
的平均數）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數
，若在定義域內存在實數
，滿足
，則稱
為“局部奇函數”．
為定義在
上的“局部奇函數”；
曲線
與
軸交于不同的兩點；
若
為假命題， 
為真命題，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一次水下考古活動中，某一潛水員需潛水
米到水底進行考古作業.其用氧量包含一下三個方面：①下潛平均速度為
米/分鐘，每分鐘用氧量為
升；②水底作業時間范圍是最少
分鐘最多
分鐘，每分鐘用氧量為
升；③返回水面時，平均速度為
米/分鐘，每分鐘用氧量為
升.潛水員在此次考古活動中的總用氧量為
升.
（1）如果水底作業時間是
分鐘，將
表示為
的函數；
（2）若
，水底作業時間為
分鐘，求總用氧量
的取值范圍；
（3）若潛水員攜帶氧氣
升，請問潛水員最多在水下多少分鐘（結果取整數）？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖已知
是邊長為
的正方形
的中心，點
分別是
的中點，沿對角線
把正方形
折成二面角
.
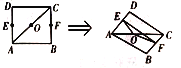
（1）證明：四面體
的外接球的體積為定值，并求出定值；
（2）若二面角
為直二面角，求二面角
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
