
(本小題滿分10分)選修4-5:不等式選講
已知函數 ,
,
(1)當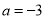 時,求不等式
時,求不等式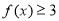 的解集;
的解集;
(2)若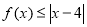 的解集包含
的解集包含 ,求
,求 的取值范圍.
的取值范圍.
(1){x|x?1}∪{x|x?4};(2)[-3,0].
【解析】
試題分析:(1)當a=-3時, 根據分段函數的特點,即可求出f(x)?3的解集;(2)f(x)?|x-4|?|x-4|-|x-2|?|x+a|.當x?[1,2]時,|x-4|-|x-2|?|x+a|?-2-a?x?2-a,可求出滿足條件的a的取值范圍.
根據分段函數的特點,即可求出f(x)?3的解集;(2)f(x)?|x-4|?|x-4|-|x-2|?|x+a|.當x?[1,2]時,|x-4|-|x-2|?|x+a|?-2-a?x?2-a,可求出滿足條件的a的取值范圍.
試題解析:(1)當a=-3時,
當x?2時,由f(x)?3得-2x+5?3,解得:x?1
當2<x<3時,f(x)?3無解;
當x?3時,由f(x)?3得2x-5?3,解得x?4;
所以f(x)?3的解集為{x|x?1}∪{x|x?4} 5分
(2)f(x)?|x-4|?|x-4|-|x-2|?|x+a|.
當x?[1,2]時,|x-4|-|x-2|?|x+a|? (4-x)-(2-x)?|x+a|? -2-a?x?2-a
由條件得:-2-a?1且2-a?2,即-3?a?0
故滿足條件的a的取值范圍為[-3,0] 10分.
考點:絕對值函數.


科目:高中數學 來源: 題型:
| A、?x≤0,都有x2-x>0 | B、?x>0,都有x2-x≤0 | C、?x>0,使得x2-x<0 | D、?x≤0,使得x2-x>0 |
查看答案和解析>>
科目:高中數學 來源:2015屆遼寧省五校協作體高三上學期期中考試理科數學試卷(解析版) 題型:選擇題
已知函數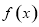 在
在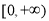 上可導,其導函數記作
上可導,其導函數記作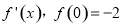 ,且
,且 ,當
,當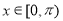 時,
時, ,若方程
,若方程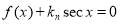 在[0,+∞)上有n個解,則數列
在[0,+∞)上有n個解,則數列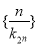 的前n項和為( )
的前n項和為( )
A.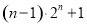 B.
B.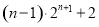 C.
C.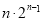 D.
D.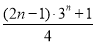
查看答案和解析>>
科目:高中數學 來源:2015屆遼寧省五校協作體高三上學期期中考試文科數學試卷(解析版) 題型:解答題
(本小題滿分12分)如圖, 四棱柱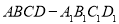 的底面ABCD是正方形,
的底面ABCD是正方形,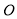 為底面中心,
為底面中心,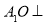 平面
平面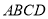 ,
,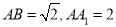 .
.

(1)證明: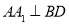 ;
;
(2)證明: 平面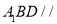 平面
平面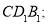
(3)求三棱柱 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源:2015屆遼寧省五校協作體高三上學期期中考試文科數學試卷(解析版) 題型:選擇題
已知 為等差數列,
為等差數列, 為數列
為數列 的前n項和,若
的前n項和,若 對一切
對一切 都成立,則首項a1的取值范圍是( )
都成立,則首項a1的取值范圍是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2015屆福建省福州市高三上學期第三次質檢理科數學試卷(解析版) 題型:解答題
(本小題滿分14分)已知函數 的導函數是
的導函數是 ,
, 在
在 處取得極值,且
處取得極值,且 ,
,
(1)求 的極大值和極小值;
的極大值和極小值;
(2)記 在閉區間
在閉區間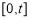 上的最大值為
上的最大值為 ,若對任意的
,若對任意的
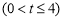 總有
總有
 成立,求
成立,求 的取值范圍;
的取值范圍;
(Ⅲ)設 是曲線
是曲線 上的任意一點.當
上的任意一點.當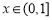 時,求直線OM斜率的最小值,據此判斷
時,求直線OM斜率的最小值,據此判斷 與
與 的大小關系,并說明理由.
的大小關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com