
【題目】已知產品![]() 的質量采用綜合指標值
的質量采用綜合指標值![]() 進行衡量,
進行衡量,![]() 為一等品;
為一等品;![]() 為二等品;
為二等品;![]() 為三等品.我市一家工廠準備購進新型設備以提高生產產品
為三等品.我市一家工廠準備購進新型設備以提高生產產品![]() 的效益,在某供應商提供的設備中任選一個試用,生產了一批產品并統計相關數據,得到頻率分布直方圖:
的效益,在某供應商提供的設備中任選一個試用,生產了一批產品并統計相關數據,得到頻率分布直方圖:
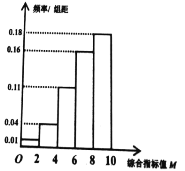
(1)估計該新型設備生產的產品![]() 為二等品的概率;
為二等品的概率;
(2)根據這家工廠的記錄,產品各等次的銷售率(某等次產品銷量與其對應產量的比值)及單件售價情況如下:
一等品 | 二等品 | 三等品 | |
銷售率 |
|
|
|
單件售價 |
|
|
|
根據以往的銷售方案,未售出的產品統一按原售價的![]() 全部處理完.已知該工廠認購該新型設備的前提條件是,該新型設備生產的產品同時滿足下列兩個條件:
全部處理完.已知該工廠認購該新型設備的前提條件是,該新型設備生產的產品同時滿足下列兩個條件:
①綜合指標值的平均數不小于![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
②單件平均利潤值不低于![]() .
.
若該新型設備生產的產品![]() 的成本為
的成本為![]() 元/件,月產量為
元/件,月產量為![]() 件,在銷售方案不變的情況下,根據以上圖表數據,分析該新型設備是否達到該工廠的認購條件.
件,在銷售方案不變的情況下,根據以上圖表數據,分析該新型設備是否達到該工廠的認購條件.
【答案】(1) 事件![]() 的概率估計值為
的概率估計值為![]() ;(2)見解析.
;(2)見解析.
【解析】分析:(1)根據頻率分布直方圖中的頻率計算即可.(2)根據頻率分布直方圖求出綜合指標值的平均數,然后再根據題意求出單件平均利潤值,根據題意進行判斷可得結論.
詳解:(1)記![]() 為事件“該新型設備生產的產品
為事件“該新型設備生產的產品![]() 為二等品”.
為二等品”.
由直方圖可知,該新型設備生產的產品![]() 為二等品的頻率為:
為二等品的頻率為:
![]() ,
,
故事件![]() 的概率估計值為
的概率估計值為![]() .
.
(2)①先分析該新型設備生產的產品![]() 的綜合指標值的平均數:
的綜合指標值的平均數:
由直方圖可知綜合指標值的平均數
![]()
![]() .
.
所以該設備生產出的產品![]() 的綜合指標值的平均數的估計值
的綜合指標值的平均數的估計值![]() ,
,
故滿足認購條件①.
②再分析該窯爐燒制的單件平均利潤值:
由直方圖可知該設備生產出的產品![]() 為一、二、三等品的概率估計值分別為:
為一、二、三等品的概率估計值分別為:![]() ,
,![]() ,
,![]() .
.
故![]() 件產品中,一、二、三等品的件數估計值分別為:
件產品中,一、二、三等品的件數估計值分別為:![]() 件,
件,![]() 件,
件,![]() 件.
件.
一等品的銷售總利潤為![]() 元;
元;
二等品的銷售總利潤為![]() 元;
元;
三等品的銷售總利潤為![]() 元.
元.
故![]() 件產品的單件平均利潤值的估計值為:
件產品的單件平均利潤值的估計值為:
![]() 元.
元.
滿足認購條件②.
綜上所述,該新型設備達到認購條件.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知曲線C的參數方程為 ![]() (α為參數),以直角坐標系原點為極點,Ox軸正半軸為極軸建立極坐標系.
(α為參數),以直角坐標系原點為極點,Ox軸正半軸為極軸建立極坐標系.
(1)求曲線C的極坐標方程
(2)若直線l的極坐標方程為ρ(sinθ+cosθ)=1,求直線l被曲線C截得的弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:噸)的影響,對近六年的年宣傳費
(單位:噸)的影響,對近六年的年宣傳費![]() 和年銷售量
和年銷售量![]() (
(![]() )的數據作了初步統計,得到如下數據:
)的數據作了初步統計,得到如下數據:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年宣傳費 | 23 | 25 | 27 | 29 | 32 | 35 |
年銷售量 | 11 | 21 | 24 | 66 | 115 | 325 |
(1)根據散點圖判斷![]() 與
與![]() ,哪一個更適合作為年銷售量
,哪一個更適合作為年銷售量![]() (噸)與關于宣傳費
(噸)與關于宣傳費![]() (萬元)的回歸方程類型;
(萬元)的回歸方程類型;
(2)規定當產品的年銷售量![]() (噸)與年宣傳費
(噸)與年宣傳費![]() (萬元)的比值大于1時,認為該年效益良好,現從這6年中任選3年,記其中選到效益良好的數量為
(萬元)的比值大于1時,認為該年效益良好,現從這6年中任選3年,記其中選到效益良好的數量為![]() ,試求
,試求![]() 的所有取值情況及對應的概率;
的所有取值情況及對應的概率;
(3)根據頻率分布直方圖中求出樣本數據平均數的思想方法,求![]() 的平均數.
的平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
: ![]() 過圓上任意一點
過圓上任意一點![]() 向
向![]() 軸引垂線垂足為
軸引垂線垂足為![]() (點
(點![]() 、
、![]() 可重合),點
可重合),點![]() 為
為![]() 的中點.
的中點.
(1)求![]() 的軌跡方程;
的軌跡方程;
(2)若點![]() 的軌跡方程為曲線
的軌跡方程為曲線![]() ,不過原點
,不過原點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,滿足直線
兩點,滿足直線![]() ,
, ![]() ,
, ![]() 的斜率依次成等比數列,求
的斜率依次成等比數列,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() sinxcosx+sin2x+
sinxcosx+sin2x+ ![]() (x∈R).
(x∈R).
(Ⅰ)當x∈[﹣ ![]() ,
, ![]() ]時,求f(x)的最大值.
]時,求f(x)的最大值.
(Ⅱ)設△ABC的內角A,B,C所對的邊分別為a,b,c,且c= ![]() ,f(C)=2,sinB=2sinA,求a.
,f(C)=2,sinB=2sinA,求a.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 中心在坐標原點,焦點在坐標軸上,且經過
中心在坐標原點,焦點在坐標軸上,且經過![]() 三點.
三點.
(1)求橢圓![]() 的方程;
的方程;
(2)在直線![]() 上任取一點
上任取一點![]() ,連接
,連接![]() ,分別與橢圓
,分別與橢圓![]() 交于
交于![]() 兩點,判斷直線
兩點,判斷直線![]() 是否過定點?若是,求出該定點.若不是,請說明理由.
是否過定點?若是,求出該定點.若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直線![]() 與圓
與圓 ![]() 且與橢圓
且與橢圓![]() 相交于
相交于![]() 兩點.
兩點.

(1)若直線![]() 恰好經過橢圓的左頂點,求弦長
恰好經過橢圓的左頂點,求弦長![]()
(2)設直線![]() 的斜率分別為
的斜率分別為![]() ,判斷
,判斷![]() 是否為定值,并說明理由
是否為定值,并說明理由
(3)求![]() ,面積的最小值.
,面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
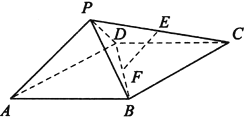
【題目】如圖,四棱錐P—ABCD中,ABCD為矩形,△PAD為等腰直角三角形,
∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分別為PC和BD的中點.
(1)證明:EF∥面PAD;
(2)證明:面PDC⊥面PAD;
(3)求四棱錐P—ABCD的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com