
【題目】已知函數f(x)= ![]() sinxcosx+sin2x+
sinxcosx+sin2x+ ![]() (x∈R).
(x∈R).
(Ⅰ)當x∈[﹣ ![]() ,
, ![]() ]時,求f(x)的最大值.
]時,求f(x)的最大值.
(Ⅱ)設△ABC的內角A,B,C所對的邊分別為a,b,c,且c= ![]() ,f(C)=2,sinB=2sinA,求a.
,f(C)=2,sinB=2sinA,求a.
【答案】解:(Ⅰ)函數f(x)= ![]() sinxcosx+sin2x+
sinxcosx+sin2x+ ![]()
= ![]() sin2x+
sin2x+ ![]() +
+ ![]()
= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+1
cos2x+1
=sin(2x﹣ ![]() )+1(x∈R),
)+1(x∈R),
當x∈[﹣ ![]() ,
, ![]() ]時,2x﹣
]時,2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
令2x﹣ ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
此時sin(2x﹣ ![]() )=1,
)=1,
f(x)取得最大值f(x)max=2;
(Ⅱ)∵f(C)=sin(2C﹣ ![]() )+1=2,
)+1=2,
∴ ![]() ,
,
∵0<C<π,∴ ![]() ,
,
令 ![]() ,
,
解得 ![]() ;
;
又∵sinB=2sinA,
∴ ![]() ,
,
∴b=2a;由余弦定理得:c2=a2+b2﹣2abcos ![]() =3,
=3,
幾a2+b2﹣ab=3,
整理得5a2﹣2a﹣3=0,
解得a=1或a=﹣ ![]() (不合題意,舍去),
(不合題意,舍去),
∴a的值是1.
【解析】(Ⅰ)化簡函數f(x)為正弦型函數,根據x∈[﹣ ![]() ,
, ![]() ],求出2x﹣
],求出2x﹣ ![]() 的范圍,從而求出f(x)的最大值;(Ⅱ)根據f(C)=2求出C的值,再由正弦、余弦定理,即可求出a的值.
的范圍,從而求出f(x)的最大值;(Ⅱ)根據f(C)=2求出C的值,再由正弦、余弦定理,即可求出a的值.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
【題目】某城市100戶居民的月平均用電量(單位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分組的頻率分布直方圖如圖所示.

(1)求直方圖中x的值;
(2)求月平均用電量的眾數和中位數;
(3)在月平均用電量為[220,240),[240,260),[260,280),[280,300]的四組用戶中,用分層抽樣的方法抽取11戶居民,則月平均用電量在[220,240)的用戶中應抽取多少戶?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班同學利用春節進行社會實踐,對本地![]() 歲的人群隨機抽取
歲的人群隨機抽取![]() 人進行了一次生活習慣是否符合低碳觀念的調查,將生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,得到如下統計表和各年齡段人數頻率分布直方圖。
人進行了一次生活習慣是否符合低碳觀念的調查,將生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,得到如下統計表和各年齡段人數頻率分布直方圖。

(一)人數統計表: (二)各年齡段人數頻率分布直方圖:
(Ⅰ)在答題卡給定的坐標系中補全頻率分布直方圖,并求出![]() 、
、![]() 、
、![]() 的值;
的值;
(Ⅱ)從![]() 歲年齡段的“低碳族”中采用分層抽樣法抽取
歲年齡段的“低碳族”中采用分層抽樣法抽取![]() 人參加戶外低碳體驗活動。若將這
人參加戶外低碳體驗活動。若將這![]() 個人通過抽簽分成甲、乙兩組,每組的人數相同,求
個人通過抽簽分成甲、乙兩組,每組的人數相同,求![]() 歲中被抽取的人恰好又分在同一組的概率。
歲中被抽取的人恰好又分在同一組的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知產品![]() 的質量采用綜合指標值
的質量采用綜合指標值![]() 進行衡量,
進行衡量,![]() 為一等品;
為一等品;![]() 為二等品;
為二等品;![]() 為三等品.我市一家工廠準備購進新型設備以提高生產產品
為三等品.我市一家工廠準備購進新型設備以提高生產產品![]() 的效益,在某供應商提供的設備中任選一個試用,生產了一批產品并統計相關數據,得到頻率分布直方圖:
的效益,在某供應商提供的設備中任選一個試用,生產了一批產品并統計相關數據,得到頻率分布直方圖:
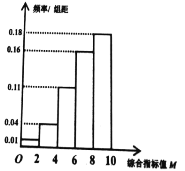
(1)估計該新型設備生產的產品![]() 為二等品的概率;
為二等品的概率;
(2)根據這家工廠的記錄,產品各等次的銷售率(某等次產品銷量與其對應產量的比值)及單件售價情況如下:
一等品 | 二等品 | 三等品 | |
銷售率 |
|
|
|
單件售價 |
|
|
|
根據以往的銷售方案,未售出的產品統一按原售價的![]() 全部處理完.已知該工廠認購該新型設備的前提條件是,該新型設備生產的產品同時滿足下列兩個條件:
全部處理完.已知該工廠認購該新型設備的前提條件是,該新型設備生產的產品同時滿足下列兩個條件:
①綜合指標值的平均數不小于![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
②單件平均利潤值不低于![]() .
.
若該新型設備生產的產品![]() 的成本為
的成本為![]() 元/件,月產量為
元/件,月產量為![]() 件,在銷售方案不變的情況下,根據以上圖表數據,分析該新型設備是否達到該工廠的認購條件.
件,在銷售方案不變的情況下,根據以上圖表數據,分析該新型設備是否達到該工廠的認購條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線過點P![]() 且與x軸、y軸的正半軸分別交于A,B兩點,O為坐標原點,是否存在這樣的直線滿足下列條件:①△AOB的周長為12;②△AOB的面積為6.若存在,求出方程;若不存在,請說明理由.
且與x軸、y軸的正半軸分別交于A,B兩點,O為坐標原點,是否存在這樣的直線滿足下列條件:①△AOB的周長為12;②△AOB的面積為6.若存在,求出方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①存在實數x,使 ![]() ;
;
②若α,β是第一象限角,且α>β,則cosα<cosβ;
③函數y=sin2x的圖象向左平移 ![]() 個單位,得到函數
個單位,得到函數 ![]() 的圖象;
的圖象;
④定義在R上的奇函數f(x)滿足f(x+2)=f(﹣x),當0≤x≤1時,f(x)=2x,
則f(2015)=﹣2.
其中正確命題是(寫出所有正確命題的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() sinωx+cosωx(ω>0)的圖象與直線y=﹣2的兩個相鄰公共點之間的距離等于π,則f(x)的單調遞減區間是( )
sinωx+cosωx(ω>0)的圖象與直線y=﹣2的兩個相鄰公共點之間的距離等于π,則f(x)的單調遞減區間是( )
A.[kπ+ ![]() ,kπ+
,kπ+ ![]() ],k∈z
],k∈z
B.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈z
],k∈z
C.[2kπ+ ![]() ,2kπ+
,2kπ+ ![]() ],k∈z
],k∈z
D.[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈z
],k∈z
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com