
【題目】設數列![]() 滿足:
滿足:![]() ,
,![]() (其中
(其中![]() 為非零實常數).
為非零實常數).
(1)設![]() ,求證:數列
,求證:數列![]() 是等差數列,并求出通項公式;
是等差數列,并求出通項公式;
(2)設![]() ,記
,記![]() ,求使得不等式
,求使得不等式![]() 成立的最小正整數
成立的最小正整數![]() ;
;
(3)若![]() ,對于任意的正整數
,對于任意的正整數![]() ,均有
,均有![]() ,當
,當![]() 、
、![]() 、
、![]() 依次成等比數列時,求
依次成等比數列時,求![]() 、
、![]() 、
、![]() 的值.
的值.
【答案】(1)![]() ,見解析;(2)10;(3)見解析
,見解析;(2)10;(3)見解析
【解析】
(1)![]() 時,根據定義可證數列是等差數列,根據等差數列的通項公式可求;
時,根據定義可證數列是等差數列,根據等差數列的通項公式可求;
(2)![]() 時,將已知變形可得數列
時,將已知變形可得數列![]() 是等比數列,可得
是等比數列,可得![]() 的通項公式,
的通項公式,
可得![]() 的通項公式,再求和解不等式可得;
的通項公式,再求和解不等式可得;
(3)![]() 且
且![]() 時,將已知變形為
時,將已知變形為![]() ,可得數列
,可得數列![]() 為等比數列,可求得
為等比數列,可求得![]() ,再根據數列
,再根據數列![]() 遞增可求得
遞增可求得![]() ,再由
,再由![]() 、
、![]() 、
、![]() 依次成等比數列,可得
依次成等比數列,可得![]() ,因為
,因為![]() ,所以只能是
,所以只能是![]() .
.
(1)證明:![]() 時,由
時,由![]() 得
得![]() ,
,
所以數列![]() 是首項為
是首項為![]() ,公差為
,公差為![]() 的等差數列,
的等差數列,
所以![]() .
.
(2)![]() 時,由
時,由![]() 得
得![]() .
.
因為![]() ,所以數列
,所以數列![]() 是首項為1,公比為
是首項為1,公比為![]() 的等比數列,
的等比數列,
所以![]()
![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]()
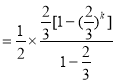
![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]()
![]()
![]() .
.
所以使得不等式![]() 成立的最小正整數
成立的最小正整數![]() 為10.
為10.
(3)![]() 時,由
時,由![]() ,得
,得![]() ,
,
得![]() ,
,
所以![]() ,
,
所以![]() ,
,
由![]() 知
知![]() 為自然數,所以
為自然數,所以![]()
![]() ,
,
又對于任意的正整數![]() ,均有
,均有![]() ,
,
所以數列![]() 為遞增數列,
為遞增數列,
所以![]() ,又
,又![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
因為![]() 、
、![]() 、
、![]() 依次成等比數列,
依次成等比數列,
所以![]() ,
,
即![]() .
.
即![]() ,
,
因為![]() ,
,![]() ,
,![]() ,
,
所以只能有![]() ,
,
所以![]() ,
,
綜上![]() .
.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:
【題目】某校抽取了100名學生期中考試的英語和數學成績,已知成績都不低于100分,其中英語成績的頻率分布直方圖如圖所示,成績分組區間是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
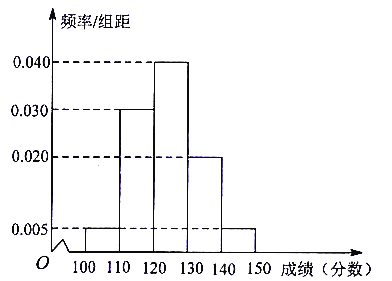
(1)根據頻率分布直方圖,估計這100名學生英語成績的平均數和中位數(同一組數據用該區間的中點值作代表);
(2)若這100名學生數學成績分數段的人數y的情況如下表所示:
分組區間 |
|
|
|
|
|
y | 15 | 40 | 40 | m | n |
且區間![]() 內英語人數與數學人數之比為
內英語人數與數學人數之比為![]() ,現從數學成績在
,現從數學成績在![]() 的學生中隨機選取2人,求選出的2人中恰好有1人數學成績在
的學生中隨機選取2人,求選出的2人中恰好有1人數學成績在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某市有相交于點O的一條東西走向的公路l,與南北走向的公路m,這兩條公路都與一塊半徑為1(單位:千米)的圓形商城A相切.根據市民建議,欲再新建一條公路PQ,點P、Q分別在公路l、m上,且要求PQ與圓形商城A也相切.
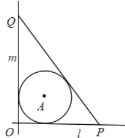
(1)當P距O處4千米時,求OQ的長;
(2)當公路PQ長最短時,求OQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為踐行“綠水青山就是金山銀山”的發展理念,某城區對轄區內![]() ,
,![]() ,
,![]() 三類行業共200個單位的生態環境治理成效進行了考核評估,考評分數達到80分及其以上的單位被稱為“星級”環保單位,未達到80分的單位被稱為“非星級”環保單位.現通過分層抽樣的方法獲得了這三類行業的20個單位,其考評分數如下:
三類行業共200個單位的生態環境治理成效進行了考核評估,考評分數達到80分及其以上的單位被稱為“星級”環保單位,未達到80分的單位被稱為“非星級”環保單位.現通過分層抽樣的方法獲得了這三類行業的20個單位,其考評分數如下:
![]() 類行業:85,82,77,78,83,87;
類行業:85,82,77,78,83,87;
![]() 類行業:76,67,80,85,79,81;
類行業:76,67,80,85,79,81;
![]() 類行業:87,89,76,86,75,84,90,82.
類行業:87,89,76,86,75,84,90,82.
(Ⅰ)計算該城區這三類行業中每類行業的單位個數;
(Ⅱ)若從抽取的![]() 類行業這6個單位中,再隨機選取3個單位進行某項調查,求選出的這3個單位中既有“星級”環保單位,又有“非星級”環保單位的概率.
類行業這6個單位中,再隨機選取3個單位進行某項調查,求選出的這3個單位中既有“星級”環保單位,又有“非星級”環保單位的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() ,且經過點
,且經過點![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 作一條斜率不為
作一條斜率不為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,記點
兩點,記點![]() 關于
關于![]() 軸對稱的點為
軸對稱的點為![]() .證明:直線
.證明:直線![]() 經過
經過![]() 軸上一定點
軸上一定點![]() ,并求出定點
,并求出定點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學采取分層抽樣的方法從應屆高三學生中按照性別抽取20名學生,其中8名女生中有3名報考理科,男生中有2名報考文科.
(1)根據以上信息,寫出![]() 列聯表;
列聯表;
(2)用假設檢驗的方法分析有多大的把握認為該中學的高三學生選報文理科與性別有關?
參考公式:![]()
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)試求函數![]() 的極值點的個數;
的極值點的個數;
(2)若![]() ,
,![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
參考數據:
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.558 | 2.303 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3-3x及y=f(x)上一點P(1,-2),過點P作直線l.
(1)求使直線l和y=f(x)相切且以P為切點的直線方程;
(2)求使直線l和y=f(x)相切且切點異于點P的直線方程y=g(x).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市春節期間7家超市的廣告費支出![]() (萬元)和銷售額
(萬元)和銷售額![]() (萬元)數據如下:
(萬元)數據如下:
超市 | A | B | C | D | E | F | G |
廣告費支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
銷售額 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
參數數據及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,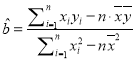 ,
,![]() ,
,![]() .
.
(1)若用線性回歸模型擬合y與x的關系,求y關于x的線性回歸方程;
(2)用對數回歸模型擬合y與x的關系,可得回歸方程:![]() ,經計算得出線性回歸模型和對數模型的
,經計算得出線性回歸模型和對數模型的![]() 分別約為0.75和0.97,請用
分別約為0.75和0.97,請用![]() 說明選擇哪個回歸模型更合適,并用此模型預測A超市廣告費支出為8萬元時的銷售額.
說明選擇哪個回歸模型更合適,并用此模型預測A超市廣告費支出為8萬元時的銷售額.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com