
| A. | 充分必要條件 | B. | 必要不充分條件 | ||
| C. | 充分不必要條件 | D. | 既不充分也不必要條件 |
分析 根據題意,先求出直線y=kx+2與圓x2+y2=1相切時k的值,進而分析可得條件p是條件q的充分不必要條件,結合充要條件的性質可得¬p是¬q的必要不充分條件,即可得答案.
解答 解:根據題意,若直線y=kx+2與圓x2+y2=1相切,
則有$\frac{|2|}{\sqrt{1+{k}^{2}}}$=1,
解可得k=±$\sqrt{3}$,
若有k=$\sqrt{3}$,則有直線y=kx+2與圓x2+y2=1相切,而直線y=kx+2與圓x2+y2=1相切,不一定有k=$\sqrt{3}$,
故條件p:k=$\sqrt{3}$是條件q:直線y=kx+2與圓x2+y2=1相切成立的充分不必要條件,
則¬p是¬q的必要不充分條件,
故選:B.
點評 本題考查充分、必要條件的判定,關鍵是依據直線與圓的位置關系求出k的值.


科目:高中數學 來源: 題型:解答題
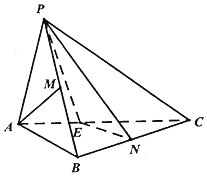 如圖,三棱錐P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,點M,N分別為PB,BC的中點.
如圖,三棱錐P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,點M,N分別為PB,BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 不存在x0∈R,${x_0}^2-2{x_0}+1≥0$ | B. | 存在x0∈R,${x_0}^2-2{x_0}+1≤0$ | ||
| C. | 存在x0∈R,${x_0}^2-2{x_0}+1<0$ | D. | 對任意的x∈R,x2-2x+1<0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com