
【題目】已知![]() 與函數
與函數![]() 和
和![]() 都相切,則不等式組
都相切,則不等式組![]() 所確定的平面區域在
所確定的平面區域在![]() 內的面積為( )
內的面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根據直線![]() 與
與![]() 和
和![]() 都相切,求得
都相切,求得![]() 的值,由此畫出不等式組所表示的平面區域以及圓
的值,由此畫出不等式組所表示的平面區域以及圓![]() ,由此求得正確選項.
,由此求得正確選項.
![]() .設直線
.設直線![]() 與
與![]() 相切于點
相切于點![]() ,斜率為
,斜率為![]() ,所以切線方程為
,所以切線方程為![]() ,化簡得
,化簡得![]() ①.令
①.令![]() ,解得
,解得![]() ,
,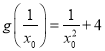 ,所以切線方程為
,所以切線方程為 ,化簡得
,化簡得![]() ②.由①②對比系數得
②.由①②對比系數得![]() ,化簡得
,化簡得![]() ③.構造函數
③.構造函數![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,所以
上遞增,所以![]() 在
在![]() 處取得極小值也即是最小值,而
處取得極小值也即是最小值,而![]() ,所以
,所以![]() 有唯一解.也即方程③有唯一解
有唯一解.也即方程③有唯一解![]() .所以切線方程為
.所以切線方程為![]() .即
.即![]() .不等式組
.不等式組![]() 即
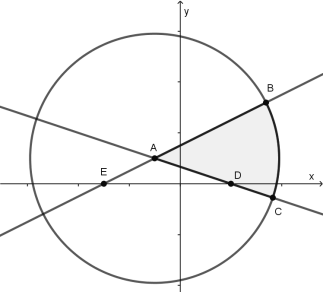
即![]() ,畫出其對應的區域如下圖所示.圓
,畫出其對應的區域如下圖所示.圓![]() 可化為
可化為![]() ,圓心為
,圓心為![]() .而方程組
.而方程組![]() 的解也是
的解也是![]() .畫出圖像如下圖所示,不等式組
.畫出圖像如下圖所示,不等式組![]() 所確定的平面區域在
所確定的平面區域在![]() 內的部分如下圖陰影部分所示.直線
內的部分如下圖陰影部分所示.直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() .所以
.所以![]()
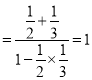 ,所以
,所以![]() ,而圓
,而圓![]() 的半徑為
的半徑為![]() ,所以陰影部分的面積是
,所以陰影部分的面積是![]() .
.
故選:B


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:高中數學 來源: 題型:
【題目】某市2013年至2019年新能源汽車y(單位:百臺)的數據如下表:

(Ⅰ)求y關于x的線性回歸方程,并預測該市2021年新能源汽車臺數;
(Ⅱ)該市某公司計劃投資600臺“雙槍同充”(兩把充電槍)、“一拖四群充”(四把充電槍)的兩種型號的直流充電樁.按要求,充電槍的總把數不少于該市2021年新能源汽車預測臺數,若雙槍同充、一拖四群充的每把充電槍的日利潤分別為25元,10元,問兩種型號的充電樁各安裝多少臺時,才能使日利潤最大,求出最大日利潤.![]()
附:回歸直線的斜率和截距的最小二乘法估計公式分別為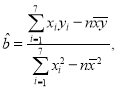
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新疆小南瓜以沙甜聞名全國,小田計劃從新疆運輸小南瓜去上海,隨機從某瓜農的瓜地里挑選了100個,其質量分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:克)中,經統計得頻率分布直方圖如圖所示,將頻率視為概率.
(單位:克)中,經統計得頻率分布直方圖如圖所示,將頻率視為概率.
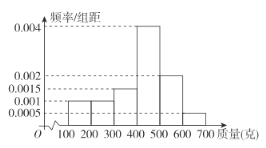
(1)請根據頻率分布直方圖估計該瓜農的小南瓜的平均質量;
(2)已知瓜地里還有2萬個小南瓜已經成熟,可以采摘,小田想全部購買,可是瓜農要求超過400克的小南瓜以5元一個的價格出售,其他的以3元一個的價格出售.將頻率視為概率,若新疆到上海往返的運費約2000元,請問這2萬個小南瓜在上海以每斤(500克)多少元定價才能保證小田的利潤不少于5000元?(結果保留一位小數)
(3)某天王阿姨在上海某超市的蔬菜柜臺上看到小田從新疆采摘的新疆小南瓜,已知柜臺上有若干個,若質量超過500克的小南瓜為“優質品”,王阿姨隨機購買了20個小南瓜,求王阿姨購買的小南瓜中“優質品”個數的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校![]() 名學生參加軍事冬令營活動,活動期間各自扮演一名角色進行分組游戲,角色按級別從小到大共
名學生參加軍事冬令營活動,活動期間各自扮演一名角色進行分組游戲,角色按級別從小到大共![]() 種,分別為士兵、排長、連長、營長、團長、旅長、師長、軍長和司令.游戲分組有兩種方式,可以
種,分別為士兵、排長、連長、營長、團長、旅長、師長、軍長和司令.游戲分組有兩種方式,可以![]() 人一組或者
人一組或者![]() 人一組.如果
人一組.如果![]() 人一組,則必須角色相同;如果
人一組,則必須角色相同;如果![]() 人一組,則
人一組,則![]() 人角色相同或者
人角色相同或者![]() 人為級別連續的
人為級別連續的![]() 個不同角色.已知這
個不同角色.已知這![]() 名學生扮演的角色有
名學生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,現在新加入
人,現在新加入![]() 名學生,將這
名學生,將這![]() 名學生分成
名學生分成![]() 組進行游戲,則新加入的學生可以扮演的角色的種數為________.
組進行游戲,則新加入的學生可以扮演的角色的種數為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)解關于![]() 的不等式:
的不等式:![]() ;
;
(2)當![]() 時,過點
時,過點![]() 是否存在函數
是否存在函數![]() 圖象的切線?若存在,有多少條?若不存在,說明理由;
圖象的切線?若存在,有多少條?若不存在,說明理由;
(3)若![]() 是使
是使![]() 恒成立的最小值,試比較
恒成立的最小值,試比較![]() 與
與![]() 的大小(
的大小(![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(多選題)下列說法中,正確的命題是( )
A.已知隨機變量![]() 服從正態分布
服從正態分布![]() ,
,![]() ,則
,則![]() .
.
B.以模型![]() 去擬合一組數據時,為了求出回歸方程,設
去擬合一組數據時,為了求出回歸方程,設![]() ,將其變換后得到線性方程
,將其變換后得到線性方程![]() ,則
,則![]() ,
,![]() 的值分別是
的值分別是![]() 和0.3.
和0.3.
C.已知兩個變量具有線性相關關系,其回歸直線方程為![]() ,若
,若![]() ,
,![]() ,
,![]() ,則
,則![]() .
.
D.若樣本數據![]() ,
,![]() ,…,
,…,![]() 的方差為2,則數據
的方差為2,則數據![]() ,
,![]() ,…,
,…,![]() 的方差為16.
的方差為16.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,隨著我國汽車消費水平的提高,二手車流通行業得到迅猛發展.某汽車交易市場對2017年成交的二手車交易前的使用時間(以下簡稱“使用時間”)進行統計,得到頻率分布直方圖如圖1.


圖1 圖2
(1)記“在![]() 年成交的二手車中隨機選取一輛,該車的使用年限在
年成交的二手車中隨機選取一輛,該車的使用年限在![]() ”為事件
”為事件![]() ,試估計
,試估計![]() 的概率;
的概率;
(2)根據該汽車交易市場的歷史資料,得到散點圖如圖2,其中![]() (單位:年)表示二手車的使用時間,
(單位:年)表示二手車的使用時間,![]() (單位:萬元)表示相應的二手車的平均交易價格.由散點圖看出,可采用
(單位:萬元)表示相應的二手車的平均交易價格.由散點圖看出,可采用![]() 作為二手車平均交易價格
作為二手車平均交易價格![]() 關于其使用年限
關于其使用年限![]() 的回歸方程,相關數據如下表(表中
的回歸方程,相關數據如下表(表中![]() ,
,![]() ):
):

①根據回歸方程類型及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
②該汽車交易市場對使用8年以內(含8年)的二手車收取成交價格![]() 的傭金,對使用時間8年以上(不含8年)的二手車收取成交價格
的傭金,對使用時間8年以上(不含8年)的二手車收取成交價格![]() 的傭金.在圖1對使用時間的分組中,以各組的區間中點值代表該組的各個值.若以2017年的數據作為決策依據,計算該汽車交易市場對成交的每輛車收取的平均傭金.
的傭金.在圖1對使用時間的分組中,以各組的區間中點值代表該組的各個值.若以2017年的數據作為決策依據,計算該汽車交易市場對成交的每輛車收取的平均傭金.
附注:①對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ;
;
②參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我區的中小學辦學條件在政府的教育督導下,迅速得到改變.督導一年后.分別隨機抽查了高中(用![]() 表示)與初中(用
表示)與初中(用![]() 表示)各10所學校.得到相關指標的綜合評價得分(百分制)的莖葉圖如圖所示.則從莖葉圖可得出正確的信息為(80分及以上為優秀)( )
表示)各10所學校.得到相關指標的綜合評價得分(百分制)的莖葉圖如圖所示.則從莖葉圖可得出正確的信息為(80分及以上為優秀)( )
①高中得分與初中得分的優秀率相同
②高中得分與初中得分的中位數相同
③高中得分的方差比初中得分的方差大
④高中得分與初中得分的平均分相同
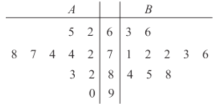
A.①②B.①③C.②④D.③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com