
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
分析 根據平面向量的數量積與向量垂直以及模長的計算公式,即可求出對應的結果.
解答 解:非零向量$\overrightarrow a$與$\overrightarrow b$滿足:$|\overrightarrow a|=2$,$(\overrightarrow a+\overrightarrow b)•\overrightarrow a=0$,
∴${\overrightarrow{a}}^{2}$+$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即$\overrightarrow{a}$•$\overrightarrow{b}$=-4;
又$(2\overrightarrow a+\overrightarrow b)⊥\overrightarrow b$,
∴(2$\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{b}$=2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=0,
∴${|\overrightarrow{b}|}^{2}$=-2$\overrightarrow{a}$•$\overrightarrow{b}$=8,
∴$|\overrightarrow b|$=2$\sqrt{2}$.
故選:D.
點評 本題主要考查了平面向量的數量積以及模長與夾角的應用問題,屬于基礎題目.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
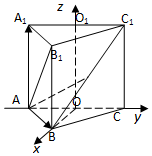 已知正三棱柱ABC-A1B1C1,底面邊長AB=2,AB1⊥BC1,點O、O1分別是邊AC,A1C1的中點,建立如圖所示的空間直角坐標系.
已知正三棱柱ABC-A1B1C1,底面邊長AB=2,AB1⊥BC1,點O、O1分別是邊AC,A1C1的中點,建立如圖所示的空間直角坐標系.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
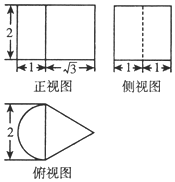
| A. | $\frac{2\sqrt{3}}{3}$+π | B. | $\frac{2\sqrt{3}}{3}$+2π | C. | 2 $\sqrt{3}$+2π | D. | 2 $\sqrt{3}$+π |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com