
【題目】已知函數f(x)=x2+bx+c,(b,c∈R),集合A={x丨f(x)=0},B={x|f(f(x))=0},若存在x0∈B,x0A則實數b的取值范圍是( )
A.b≠0
B.b<0或b≥4
C.0≤b<4
D.b≤4或b≥4
【答案】B
【解析】解:由題意可得,A是函數f(x)的零點構成的集合. 由f(f(x))=0,可得 (x2+bx+c)2+b(x2+bx+c)+c=0,把x2+bx+c=0代入,解得c=0.
故函數f(x)=x2+bx,故由f(x)=0可得 x=0,或x=﹣b,故A={0,﹣b}.
方程f(f(x))=0,即 (x2+bx)2+b(x2+bx)=0,即 (x2+bx)(x2+bx+b)=0,
解得x=0,或x=﹣b,或 x= ![]() .
.
由于存在x0∈B,x0A,故b2﹣4b≥0,解得b≤0,或b≥4.
由于當b=0時,不滿足集合中元素的互異性,故舍去.
即實數b的取值范圍為{b|b<0或b≥4 },
故選B.
【考點精析】根據題目的已知條件,利用元素與集合關系的判斷和函數的零點的相關知識可以得到問題的答案,需要掌握對象![]() 與集合
與集合![]() 的關系是
的關系是![]() ,或者
,或者![]() ,兩者必居其一;函數的零點就是方程的實數根,亦即函數的圖象與軸交點的橫坐標.即:方程有實數根,函數的圖象與坐標軸有交點,函數有零點.
,兩者必居其一;函數的零點就是方程的實數根,亦即函數的圖象與軸交點的橫坐標.即:方程有實數根,函數的圖象與坐標軸有交點,函數有零點.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】設函數f(x)=﹣2x , g(x)=lg(ax2﹣2x+1),若對任意x1∈R,都存在x2∈R,使f(x1)=g(x2),則實數a的取值范圍為( )
A.(﹣1,0)
B.(0,1)
C.(﹣∞,1]
D.[1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() .
.
(1)設函數h(x)=g(x)﹣f(x),求函數h(x)在區間[2,4]上的值域;
(2)定義min(p,q)表示p,q中較小者,設函數H(x)=min{f(x),g(x)}(x>0), ①求函數H(x)的單調區間及最值;
②若關于x的方程H(x)=k有兩個不同的實根,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點為
的一個焦點為![]() ,其左頂點
,其左頂點![]() 在圓
在圓![]() 上.
上.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,設點
兩點,設點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() (點
(點![]() 與點
與點![]() 不重合),且直線
不重合),且直線![]() 與
與![]() 軸的交于點
軸的交于點![]() ,試問
,試問![]() 的面積是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
的面積是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ) 當a=0時,求曲線f(x)在x =1處的切線方程;
(Ⅱ) 設函數![]() ,求函數h(x)的極值;
,求函數h(x)的極值;
(Ⅲ) 若![]() 在[1,e](e=2.718 28…)上存在一點x0,使得
在[1,e](e=2.718 28…)上存在一點x0,使得![]() 成立,求a的取值范圍.
成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是矩形,側棱PD⊥底面ABCD,PD=DC,點E是PC的中點,作EF⊥PB交PB于點F. 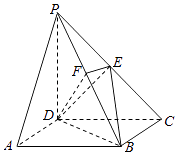
(1)求證:PA∥平面BDE;
(2)求證:PB⊥平面DEF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com