【題目】某學校為了研究期中考試前學生所做數學模擬試題的套數與考試成績的關系，統計了五個班做的模擬試卷套數量及期中考試的平均分如下：
套（x） | 7 | 6 | 6 | 5 | 6 |
數學平均分（y） | 125 | 120 | 110 | 100 | 115 |
(Ⅰ) 若x與y成線性相關，則某班做了8套模擬試題，預計平均分為多少？
（2）期中考試對學生進行獎勵，考入年級前200名，獲一等獎學金500元；考入年級201—500 名，獲二等獎學金300元；考入年級501名以后的學生生將不能獲得獎學金。甲、乙兩名學生獲一等獎學金的概率均為
，獲二等獎學金的概率均為
，.若甲、乙兩名學生獲得每個等級的獎學金是相互獨立的，求甲、乙兩名學生所獲得獎學金總金額X 的分布列及數學期望。
附： 
， 
。
文敬圖書課時先鋒系列答案科目：高中數學 來源： 題型：
【題目】十九大指出中國的電動汽車革命早已展開，通過以新能源汽車替代汽/柴油車，中國正在大力實施一項將重塑全球汽車行業的計劃．2018年某企業計劃引進新能源汽車生產設備，通過市場分析，全年需投入固定成本2500萬元，每生產x（百輛），需另投入成本
萬元，且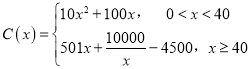
．由市場調研知，每輛車售價5萬元，且全年內生產的車輛當年能全部銷售完．
（1）求出2018年的利潤L（x）（萬元）關于年產量x（百輛）的函數關系式；（利潤=銷售額-成本）
（2）2018年產量為多少百輛時，企業所獲利潤最大?并求出最大利潤．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在“新零售”模式的背景下，某大型零售公司推廣線下分店，計劃在S市的A區開設分店，為了確定在該區開設分店的個數，該公司對該市已開設分店的其他區的數據作了初步處理后得到下列表格.記x表示在各區開設分店的個數，y表示這個x個分店的年收入之和.
(1)該公司已經過初步判斷，可用線性回歸模型擬合y與x的關系，求y關于x的線性回歸方程
(2)假設該公司在A區獲得的總年利潤z(單位:百萬元)與x，y之間的關系為
，請結合(1)中的線性回歸方程，估算該公司應在A區開設多少個分店時，才能使A區平均每個分店的年利潤最大?
(參考公式:，其中
，
)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐
的底面
為菱形，
，
底面，
，E為
的中點.
（1）求證：
平面
；
（2）求三棱錐
的體積
；
（3）在側棱
上是否存在一點M，滿足
平面
，若存在，求
的長；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4 極坐標與參數方程
在平面直角坐標系
中，曲線
的參數方程為
(其中
為參數）.以坐標原點
為極點， 
軸正半軸為極軸建立極坐標系并取相同的單位長度，圓 
的極坐標方程為
.
（1）求曲線的方程普通方程和的直角坐標方程；
（2）過圓的圓心，傾斜角為
的直線
與曲線交于A,B兩點，求
的值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了了解某學校高三年級學生的數學成績，從中抽取
名學生的數學成績（百分制）作為樣本，按成績分成
組：
，
，
，
，
，頻率分布直方圖如圖所示．成績落在中的人數為
．
（Ⅰ）求
和的值；
（Ⅱ）根據樣本估計總體的思想，估計該校高三年級學生數學成績的平均數
和中位數
；
（Ⅲ）成績在
分以上（含分）為優秀，樣本中成績落在
中的男、女生人數比為
，成績落在
中的男、女生人數比為
，完成
列聯表，并判斷是否有
的把握認為數學成績優秀與性別有關．
參考公式和數據：
．
|
|
|
|
|
|
|
|
|
|
男生 | 女生 | 合計 | |
優秀 | |||
不優秀 | |||
合計 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐S-ABCD中，底面ABCD為菱形，∠BAD=60°，平面SAD⊥平面ABCD，SA=SD，E，P，Q分別是棱AD，SC，AB的中點．
（Ⅰ）求證：PQ∥平面SAD；
（Ⅱ）求證：AC⊥平面SEQ；
（Ⅲ）如果SA=AB=2，求三棱錐S-ABC的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的左右焦點分別為
， 
，左頂點為
，上頂點為
， 
的面積為
.
（1）求橢圓
的方程；
（2）設直線
： 
與橢圓
相交于不同的兩點
， 
， 
是線段
的中點.若經過點
的直線
與直線
垂直于點
，求
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
