
【題目】如圖,在四棱錐S-ABCD中,底面ABCD為菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分別是棱AD,SC,AB的中點.
(Ⅰ)求證:PQ∥平面SAD;
(Ⅱ)求證:AC⊥平面SEQ;
(Ⅲ)如果SA=AB=2,求三棱錐S-ABC的體積.

【答案】1
【解析】
試題(Ⅰ)證明:取SD中點F,連結AF,PF.
因為 P,F分別是棱SC,SD的中點,
所以 FP∥CD,且FP=![]() CD.
CD.
又因為菱形ABCD中,Q是AB的中點,
所以 AQ∥CD,且AQ =![]() CD.
CD.
所以 FP//AQ且FP=AQ.
所以 AQPF為平行四邊形.
所以 PQ//AF.
又因為![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以 PQ//平面SAD . 5分
(Ⅱ)證明:連結BD,
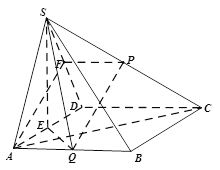
因為 △SAD中SA=SD,點E棱AD的中點,
所以 SE⊥AD.
又 平面SAD⊥平面ABCD,
平面SAD![]() 平面ABCD=AD,
平面ABCD=AD,
SE![]() 平面
平面![]() ,
,
所以 SE⊥平面ABCD,
所以SE⊥AC.
因為 底面ABCD為菱形,
E,Q分別是棱AD,AB的中點,
所以 BD⊥AC,EQ∥BD.
所以 EQ⊥AC,
因為 SE![]() EQ=E,
EQ=E,
所以 AC⊥平面SEQ. 11分
(Ⅲ)解:因為菱形ABCD中,∠BAD=60°,AB=2,
所以![]() .
.
因為SA=AD=SD=2,E是AD的中點,所以SE=![]() .
.
由(Ⅱ)可知SE⊥平面ABC,
所以三棱錐S-ABC的體積![]() =
=![]() . 14分
. 14分


科目:高中數學 來源: 題型:
【題目】某中學高一年級共8個班,現從高一年級選10名同學組成社區服務小組,其中高一(1)班選取3名同學,其它各班各選取1名同學.現從這10名同學中隨機選取3名同學,到社區老年中心參加“尊老愛老”活動(每位同學被選到的可能性相同).
(1)求選出的3名同學來自不同班級的概率;
(2)設X為選出同學中高一(1)班同學的人數,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了研究期中考試前學生所做數學模擬試題的套數與考試成績的關系,統計了五個班做的模擬試卷套數量及期中考試的平均分如下:
套(x) | 7 | 6 | 6 | 5 | 6 |
數學平均分(y) | 125 | 120 | 110 | 100 | 115 |
(Ⅰ) 若x與y成線性相關,則某班做了8套模擬試題,預計平均分為多少?
(2)期中考試對學生進行獎勵,考入年級前200名,獲一等獎學金500元;考入年級201—500 名,獲二等獎學金300元;考入年級501名以后的學生生將不能獲得獎學金。甲、乙兩名學生獲一等獎學金的概率均為![]() ,獲二等獎學金的概率均為
,獲二等獎學金的概率均為![]() ,.若甲、乙兩名學生獲得每個等級的獎學金是相互獨立的,求甲、乙兩名學生所獲得獎學金總金額X 的分布列及數學期望。
,.若甲、乙兩名學生獲得每個等級的獎學金是相互獨立的,求甲、乙兩名學生所獲得獎學金總金額X 的分布列及數學期望。
附:  ,
, ![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為了對新研發的一種產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到如下數據:
單價x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回歸直線方程![]() =bx+a;(其中
=bx+a;(其中 ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)預計在今后的銷售中,銷量與單價仍然服從(1)中的關系,且該產品的成本是4元/件,為使工廠獲得最大利潤,該產品的單價應定為多少元?(利潤=銷售收入-成本)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 為橢圓
為橢圓![]() 的右焦點,點
的右焦點,點![]() 在橢圓
在橢圓![]() 上,已知橢圓
上,已知橢圓![]() 的離心率為
的離心率為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設過右焦點![]() 的直線
的直線![]() 與橢圓相交于
與橢圓相交于![]() ,
,![]() 兩點,記
兩點,記![]() 三條邊所在直線的斜率的乘積為
三條邊所在直線的斜率的乘積為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形, ![]() 垂直于底面
垂直于底面![]() ,
, ![]() ,點
,點![]() 為線段
為線段![]() (不含端點)上一點.
(不含端點)上一點.

(1)當![]() 是線段
是線段![]() 的中點時,求
的中點時,求![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)已知二面角![]() 的正弦值為
的正弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在Rt△ABC中,已知點A(-2,0),直角頂點B(0,-2![]() ),點C在x軸上。
),點C在x軸上。
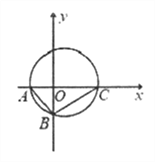
(1)求Rt△ABC外接圓的方程;
(2)求過點(-4,0)且與Rt△ABC外接圓相切的直線的方程。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司的電子新產品未上市時,原定每件售價100元,經過市場調研發現,該電子新產品市場潛力很大,該公司決定從第一周開始銷售時,該電子產品每件售價比原定售價每周漲價4元,5周后開始保持120元的價格平穩銷售,10周后由于市場競爭日益激烈,每周降價2元,直到15周結束,該產品不再銷售.
(Ⅰ)求售價![]() (單位:元)與周次
(單位:元)與周次![]() (
(![]() )之間的函數關系式;
)之間的函數關系式;
(Ⅱ)若此電子產品的單件成本![]() (單位:元)與周次
(單位:元)與周次![]() 之間的關系式為
之間的關系式為![]() ,
,![]() ,
,![]() ,試問:此電子產品第幾周的單件銷售利潤(銷售利潤
,試問:此電子產品第幾周的單件銷售利潤(銷售利潤![]() 售價
售價![]() 成本)最大?
成本)最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com