
【題目】如圖所示,在Rt△ABC中,已知點A(-2,0),直角頂點B(0,-2![]() ),點C在x軸上。
),點C在x軸上。
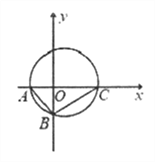
(1)求Rt△ABC外接圓的方程;
(2)求過點(-4,0)且與Rt△ABC外接圓相切的直線的方程。
【答案】(1) (x-1)2+y2=9 (2) 3x-4y+12=0或3x+4y+12=0
【解析】試題分析:(1)由題意得![]() ,得
,得![]() ,求得
,求得![]() ,進而得到圓的圓心坐標和半徑,求得圓的方程;
,進而得到圓的圓心坐標和半徑,求得圓的方程;
(2)設直線的方程為![]() ,根據直線與圓相切,圓心到直線的距離等于半徑,求得
,根據直線與圓相切,圓心到直線的距離等于半徑,求得![]() 的值,進而得到所求直線的方程.
的值,進而得到所求直線的方程.
試題解析:
(1)設點C(a,0),由AB⊥BC可得kAB·kBC=-1,即![]() ·
·![]() =-1,解得a=4.
=-1,解得a=4.
則所求的圓的圓心為AC的中點(1,0),半徑為3,
所求圓的方程為(x-1)2+y2=9.
(2)由題意知直線的斜率存在,設所求直線的方程為y=k(x+4),即kx-y+4k=0.
當直線和圓相切時,圓心到直線的距離等于半徑,所以![]() =3,解得k=
=3,解得k=![]()
![]() ,
,
所求直線的方程為y=![]() (x+4)或y=-
(x+4)或y=-![]() (x+4),
(x+4),
即3x-4y+12=0或3x+4y+12=0.


科目:高中數學 來源: 題型:
【題目】某運輸公司有7輛可載![]() 的
的![]() 型卡車與4輛可載
型卡車與4輛可載![]() 的
的![]() 型卡車,有9名駕駛員,建筑某段高速公路中,此公司承包了每天至少搬運
型卡車,有9名駕駛員,建筑某段高速公路中,此公司承包了每天至少搬運![]() 瀝青的任務,已知每輛卡車每天往返的次數為
瀝青的任務,已知每輛卡車每天往返的次數為![]() 型車8次,
型車8次, ![]() 型車6次,每輛卡車每天往返的成本費為
型車6次,每輛卡車每天往返的成本費為![]() 型車160元,
型車160元, ![]() 型車252元,每天派出
型車252元,每天派出![]() 型車和
型車和![]() 型車各多少輛,公司所花的成本費最低?
型車各多少輛,公司所花的成本費最低?
查看答案和解析>>
科目:高中數學 來源: 題型:
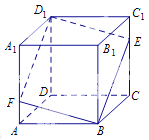
【題目】如圖所示,在正方體![]() 中,點
中,點![]() 是棱
是棱![]() 上的一個動點,平面
上的一個動點,平面![]() 交棱
交棱![]() 于點
于點![]() .給出下列命題:
.給出下列命題:
①存在點![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②對于任意的點![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在點![]() ,使得
,使得![]() 平面
平面![]() ;
;
④對于任意的點![]() ,四棱錐
,四棱錐![]() 的體積均不變.
的體積均不變.
其中正確命題的序號是______.(寫出所有正確命題的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設雙曲線C的中心為點O,若有且只有一對相交于點O,所成的角為60°的直線A1B1和A2B2,使| A1B1|=| A2B2|,其中A1,B1和A2,B2分別是這對直線與雙曲線C的交點,則該雙曲線的離心率的取值范圍是( )
A. (![]() ,2] B. [
,2] B. [![]() ,2) C. (
,2) C. (![]() ,+
,+![]() ) D. [
) D. [![]() ,+
,+![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定長為2的線段AB的兩個端點在以點(0, ![]() )為焦點的拋物線x2=2py上移動,記線段AB的中點為M,求點M到x軸的最短距離,并求此時點M的坐標。
)為焦點的拋物線x2=2py上移動,記線段AB的中點為M,求點M到x軸的最短距離,并求此時點M的坐標。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】常州地鐵項目正在緊張建設中,通車后將給市民出行帶來便利.已知某條線路通車后,地鐵的發車時間間隔 ![]() (單位:分鐘)滿足
(單位:分鐘)滿足![]() ,
,![]() .經測算,地鐵載客量與發車時間間隔
.經測算,地鐵載客量與發車時間間隔![]() 相關,當
相關,當![]() 時地鐵為滿載狀態,載客量為1200人,當
時地鐵為滿載狀態,載客量為1200人,當![]() 時,載客量會減少,減少的人數與
時,載客量會減少,減少的人數與![]() 的平方成正比,且發車時間間隔為2分鐘時的載客量為560人,記地鐵載客量為
的平方成正比,且發車時間間隔為2分鐘時的載客量為560人,記地鐵載客量為![]() .
.
⑴ 求![]() 的表達式,并求當發車時間間隔為6分鐘時,地鐵的載客量;
的表達式,并求當發車時間間隔為6分鐘時,地鐵的載客量;
⑵ 若該線路每分鐘的凈收益為![]() (元),問當發車時間間隔為多少時,該線路每分鐘的凈收益最大?
(元),問當發車時間間隔為多少時,該線路每分鐘的凈收益最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com