【題目】已知函數
．
（1）當
時，求函數
的單調遞減區間；
（2）當
時，設函數
．若函數
在區間
上有兩個零點，求實數
的取值范圍．
【答案】（1）當
時，
的單調遞減區間為
，當
時，的單調遞減區間為
，當
時，的單調遞減區間為
；（2）
.
【解析】
試題分析：（1）討論當時，當時，當時三種情況，
得增區間，
得減區間；（2）
在
上有零點，即關于
的方程
在
上有兩個不相等的實數根，可證當
時
單調遞減，當
時
單調遞增，故
.
試題解析：（1）的定義域為
，
．
①當
時，
，由
，
得
或
．
∴當
時，單調遞減．
∴的單調遞減區間為
．
②當
時，恒有
，
∴的單調遞減區間為
．
③當
時，
，由
，得
或
．
∴當
時，單調遞減．
∴的單調遞減區間為
．
綜上，當時，的單調遞減區間為；
當時，的單調遞減區間為；
當時，的單調遞減區間為．
（2）在上有零點，
即關于的方程在上有兩個不相等的實數根．
令函數
．
則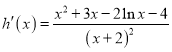
，令函數
．
則
在
上有
．
故
在上單調遞增．
∵
．
∴當時，有
即
．
∴單調遞減；
當時，有
，即
，∴單調遞增．
∵
，
，
∴
的取值范圍為．
科目：高中數學 來源： 題型：
【題目】已知直線 
：
,（1）求證：不論實數
取何值，直線 總經過一定點.為使直線不經過第二象限（2）求實數 的取值范圍（3）若直線 
與兩坐標軸的正半軸圍成的三角形面積最小，求 的方程.
（1）求證：不論實數 
取何值，直線 總經過一定點.
（2）為使直線不經過第二象限，求實數 的取值范圍.
（3）若直線 與兩坐標軸的正半軸圍成的三角形面積最小，求 的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在數列{an}中，a1=1，Sn+1=4an+2，則a2013的值為（ ）
A.3019×22012
B.3019×22013
C.3018×22012
D.無法確定
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正項等比數列{an}滿足：a7=a6+2a5 ， 若存在兩項am ， an使得 
=4a1 ， 則 
+ 
的最小值為（ ）
A.
B.
C.
D.不存在
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a＞3且a≠ 
，命題p：指數函數f（x）=（2a﹣6）x在R上單調遞減，命題q：關于x的方程x2﹣3ax+2a2+1=0的兩個實根均大于3．若p或q為真，p且q為假，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列{an}的首項a1為常數，且an+1=3n﹣2an ， （n∈N*）
（1）證明：{an﹣ 
}是等比數列；
（2）若a1= 
，{an}中是否存在連續三項成等差數列？若存在，寫出這三項，若不存在說明理由．
（3）若{an}是遞增數列，求a1的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
與拋物線
： 
相交于
， 
兩點， 
是線段
的中點，過
作
軸的垂線交
于點
.
（Ⅰ）證明：拋物線
在點
處的切線與
平行；
（Ⅱ）是否存在實數
使
？若存在，求
的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某廠每日生產一種大型產品1件，每件產品的投入成本為2000元.產品質量為一等品的概率為
，二等品的概率為
，每件一等品的出廠價為10000元，每件二等品的出廠價為8000元.若產品質量不能達到一等品或二等品，除成本不能收回外，沒生產一件產品還會帶來1000元的損失.
（1）求在連續生產3天中，恰有一天生產的兩件產品都為一等品的的概率；
（2）已知該廠某日生產的2件產品中有一件為一等品，求另一件也為一等品的概率；
（3）求該廠每日生產該種產品所獲得的利潤
（元）的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
