
【題目】將一個半徑為3分米,圓心角為α(α∈(0,2π))的扇形鐵皮焊接成一個容積為V立方分米的圓錐形無蓋容器(忽略損耗).
(1)求V關于α的函數關系式;
(2)當α為何值時,V取得最大值;
(3)容積最大的圓錐形容器能否完全蓋住桌面上一個半徑為0.5分米的球?請說明理由.
【答案】
(1)解:由題意知圓錐的母線l=3,設圓錐的底面半徑為r,則2πr=3α,
∴r= ![]() ,∴圓錐的高h=
,∴圓錐的高h= ![]() =
= ![]() =
= ![]() .
.
∴V= ![]() =
= ![]()
(2)解:V= ![]() =
= ![]()
![]() ≤
≤ ![]()
![]() =2
=2 ![]() .
.
當且僅當4π2﹣α2= ![]() 即α=
即α= ![]() 時,取等號.
時,取等號.
∴當α= ![]() 時,體積V取得最大值
時,體積V取得最大值
(3)解:當圓錐體積最大時,圓錐的底面半徑r= ![]() .
.
設圓錐軸截面△ABC的內切圓⊙O半徑為R,如圖所示,
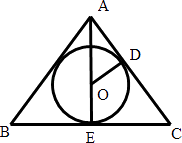
則OD=R,CD=CE= ![]() ,AC=3,∴AE=
,AC=3,∴AE= ![]() ,AD=3﹣
,AD=3﹣ ![]() .
.
由△AOD∽△ACE得 ![]() ,
,
∴ ![]() ,解得R=3
,解得R=3 ![]() ≈0.8.
≈0.8.
∵0.8>0.5,
∴容積最大的圓錐形容器能完全蓋住桌面上一個半徑為0.5分米的球.
【解析】(1)根據面積得出圓錐的底面半徑,利用勾股定理求出圓錐的高,代入體積公式即可;(2)利用基本不等式得出體積的最值及取得最值得條件;(3)求出圓錐內切球的半徑,與0.5比較大小.
【考點精析】掌握基本不等式在最值問題中的應用和旋轉體(圓柱、圓錐、圓臺)是解答本題的根本,需要知道用基本不等式求最值時(積定和最小,和定積最大),要注意滿足三個條件“一正、二定、三相等”;常見的旋轉體有:圓柱、圓錐、圓臺、球.


科目:高中數學 來源: 題型:
【題目】若![]() 是兩個相交平面,則在下列命題中,真命題的序號為 .(寫出所有真命題的序號)
是兩個相交平面,則在下列命題中,真命題的序號為 .(寫出所有真命題的序號)
①若直線![]() ,則在平面
,則在平面![]() 內,一定不存在與直線
內,一定不存在與直線![]() 平行的直線.
平行的直線.
②若直線![]() ,則在平面
,則在平面![]() 內,一定存在無數條直線與直線
內,一定存在無數條直線與直線![]() 垂直.
垂直.
③若直線![]() ,則在平面
,則在平面![]() 內,不一定存在與直線
內,不一定存在與直線![]() 垂直的直線.
垂直的直線.
④若直線![]() ,則在平面
,則在平面![]() 內,一定存在與直線
內,一定存在與直線![]() 垂直的直線.
垂直的直線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:
①函數![]() 的單調增區間是
的單調增區間是![]() ;
;
②若函數![]() 定義域為
定義域為![]() 且滿足
且滿足![]() ,則它的圖象關于
,則它的圖象關于![]() 軸對稱;
軸對稱;
③函數![]() 的值域為
的值域為![]() ;
;
④函數![]() 的圖象和直線
的圖象和直線![]() 的公共點個數是
的公共點個數是![]() ,則
,則![]() 的值可能是
的值可能是![]() ;
;
⑤若函數![]() 在
在![]() 上有零點,則實數
上有零點,則實數![]() 的取值范圍是
的取值范圍是![]() .
.
其中正確的序號是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}按三角形進行排列,如圖,第一層一個數a1 , 第二層兩個數a2和a3 , 第三層三個數a4 , a5和a6 , 以此類推,且每個數字等于下一層的左右兩個數字之和,如a1=a2+a3 , a2=a4+a5 , a3=a5+a6 , …. 
(1)若第四層四個數為0或1,a1為奇數,則第四層四個數共有多少種不同取法?
(2)若第十一層十一個數為0或1,a1為5的倍數,則第十一層十一個數共有多少種不同取法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫藥研究所開發一種新藥, 成年人按規定的劑量服用后, 每毫升血液中的含藥量![]() (微克)與時間
(微克)與時間![]() (小時)之間關系滿足如圖所示的曲線.
(小時)之間關系滿足如圖所示的曲線.
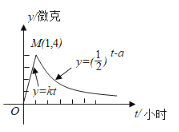
(1)寫出![]() 關于
關于![]() 的函數關系式:
的函數關系式:![]() ;
;
(2)據進一步測定: 每毫升血液中的含藥量不少于![]() 微克時, 治療疾病有效. 求服藥一次后治療疾病有效的時間.
微克時, 治療疾病有效. 求服藥一次后治療疾病有效的時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)=ex+ae﹣x為偶函數,則f(x﹣1)< ![]() 的解集為( )
的解集為( )
A.(2,+∞)
B.(0,2)
C.(﹣∞,2)
D.(﹣∞,0)∪(2,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com