
【題目】已知函數f(x)=x2+2x+alnx在區間(0,1)內無極值點,則a的取值范圍是 .
【答案】{a|a≤﹣4或a≥0}
【解析】解:函數f(x)=x2+2x+alnx在區間(0,1)內無極值函數f(x)=x2+2x+alnx在區間(0,1)內單調
函數f′(x)≥0或f′(x)≤0a∈R)在(0,1)內恒成立.
由f′(x)=2x+2 ![]() ≥0在(0,1)內恒成立
≥0在(0,1)內恒成立
a≥(﹣2x﹣2x2)max , x∈(0,1).即a≥0,
由f′(x)=2x+2 ![]() ≤0在(0,1)內恒成立
≤0在(0,1)內恒成立
a≤(﹣2x﹣2x2)min , x∈(0,1).即a≤﹣4,
所以答案是:a≤﹣4或a≥0.
所以答案是:{a|a≤﹣4或a≥0}.
【考點精析】關于本題考查的函數的極值與導數,需要了解求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值才能得出正確答案.
是極小值才能得出正確答案.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知銳角△ABC中內角A、B、C所對邊的邊長分別為a、b、c,滿足a2+b2=6abcosC,且 ![]() .
.
(1)求角C的值;
(2)設函數 ![]() ,圖象上相鄰兩最高點間的距離為π,求f(A)的取值范圍.
,圖象上相鄰兩最高點間的距離為π,求f(A)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C: ![]() 的焦點為F,直線
的焦點為F,直線![]() 與y軸的交點為P,與C的交點為Q,且
與y軸的交點為P,與C的交點為Q,且![]() .
.
(1)求C的方程;
(2)過F的直線![]() 與C相交于A,B兩點,若AB的垂直平分線
與C相交于A,B兩點,若AB的垂直平分線![]() 與C相較于M,N兩點,且A,M,B,N四點在同一圓上,求
與C相較于M,N兩點,且A,M,B,N四點在同一圓上,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB、PA、PBC分別為⊙O的切線和割線,切點A是BD的中點,AC、BD相交于點E,AB、PE相交于點F,直線CF交⊙O于另一點G、交PA于點K.

證明:(1)K是PA的中點;(2)![]() ..
..
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018河北保定市高三上學期期末調研】如圖,四面體![]() 中,
中, ![]() 、
、![]() 分別
分別![]() 、
、![]() 的中點,
的中點, ![]() ,
, ![]() .
.
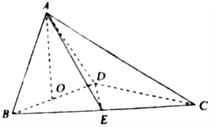
(I)求證: ![]() 平面
平面![]() ;
;
(II)求異面直線![]() 與
與![]() 所成角的余弦值的大小;
所成角的余弦值的大小;
(III)求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將一個半徑為3分米,圓心角為α(α∈(0,2π))的扇形鐵皮焊接成一個容積為V立方分米的圓錐形無蓋容器(忽略損耗).
(1)求V關于α的函數關系式;
(2)當α為何值時,V取得最大值;
(3)容積最大的圓錐形容器能否完全蓋住桌面上一個半徑為0.5分米的球?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一個工廠生產某種產品的固定成本(固定投入)為![]() 元,已知每生產
元,已知每生產![]() 件這樣的產品需要再增加成本
件這樣的產品需要再增加成本![]() (元).已知生產出的產品都能以每件
(元).已知生產出的產品都能以每件![]() 元的價格售出.
元的價格售出.
(![]() )將該廠的利潤
)將該廠的利潤![]() (元)表示為產量
(元)表示為產量![]() (件)的函數.
(件)的函數.
(![]() )要使利潤最大,該廠應生產多少件這樣的產品?最大利潤是多少?
)要使利潤最大,該廠應生產多少件這樣的產品?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 是兩條不同直線,
是兩條不同直線,![]() ,
,![]() 是兩個不同平面,則下列命題正確的是 ( )
是兩個不同平面,則下列命題正確的是 ( )
A. 若![]() ,
,![]() 垂直于同一平面,則
垂直于同一平面,則![]() 與
與![]() 平行
平行
B. 若![]() ,則
,則![]()
C. 若![]() ,
,![]() 不平行,則在
不平行,則在![]() 內不存在與
內不存在與![]() 平行的直線
平行的直線
D. 若![]() ,
,![]() 不平行,則
不平行,則![]() 與
與![]() 不可能垂直于同一平面
不可能垂直于同一平面
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com