
分析 (1)由向量數量積的坐標表示,f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=(sinωx+cosωx)(cosωx-sinωx)+$\sqrt{3}$cosωx•2sinωx,根據二倍角公式及輔助角公式即可求得f(x)=2sin(2ωx+$\frac{π}{6}$),由f(x)的最小正周期為π,即$\frac{2π}{2ω}$=π,求得ω,寫出f(x)的解析式;
(2)由f(A)=1,2sin(2A+$\frac{π}{6}$)=1,即sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$,由0<A<π,求得A=$\frac{π}{3}$,由余弦定理cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,即可求得bc的值,由三角形的面積公式即可求得△ABC的面積.
解答 解:(1)f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=(sinωx+cosωx)(cosωx-sinωx)+$\sqrt{3}$cosωx•2sinωx,
=cos2ωx-sin2ωx+2$\sqrt{3}$sinωxcosωx,
=cos2ωx+$\sqrt{3}$sin2ωx,
=2sin(2ωx+$\frac{π}{6}$),
∵f(x)的最小正周期為π.
∴$\frac{2π}{2ω}$=π,即ω=1,
∴f(x)=2sin(2x+$\frac{π}{6}$);
(2)由(1)可知:f(A)=1,即2sin(2A+$\frac{π}{6}$)=1,
∴sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$,
∵0<A<π,
∴2A+$\frac{π}{6}$=$\frac{5π}{6}$,即A=$\frac{π}{3}$,
由余弦定理可知:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{(b+c)^{2}-2bc-{a}^{2}}{2bc}$,解得:bc=20,
△ABC的面積S=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×20×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$,
△ABC的面積5$\sqrt{3}$.
點評 本題考查正弦函數圖象及性質,考查向量數量積的坐標表示,二倍角公式,輔助角公式,余弦定理及三角形的面積公式的綜合應用,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
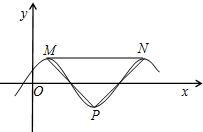 函數f(x)=$\frac{1}{2}$sin(ωx+$\frac{π}{6}$)(ω>0)的部分圖象如圖所示,設M,N是圖象上的最高點,P是圖象上的最低點,若△PMN為等腰直角三角形,則ω=( )
函數f(x)=$\frac{1}{2}$sin(ωx+$\frac{π}{6}$)(ω>0)的部分圖象如圖所示,設M,N是圖象上的最高點,P是圖象上的最低點,若△PMN為等腰直角三角形,則ω=( )| A. | 1 | B. | 2 | C. | π | D. | 2π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com