
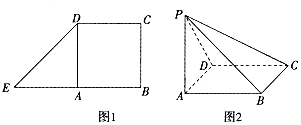
分析 (Ⅰ)推導出ABCD為平行四邊形,AD∥BC,AD⊥BE,AD⊥AB,AD⊥PA,從而AD⊥平面PAB,由此能證明AD⊥PB.
(Ⅱ)以點A為坐標原點,分別以AB,AD,AP為x,y,z軸,建立空間直角坐標系,利用向量法能求出二面角B-PC-D的大小.
解答 (Ⅰ)證明:在圖1中,∵AB∥CD,AB=CD,
∴ABCD為平行四邊形,∴AD∥BC,
∵∠B=90°,∴AD⊥BE,
當△EDA沿AD折起時,AD⊥AB,AD⊥AE,即AD⊥AB,AD⊥PA,
又AB∩PA=A,∴AD⊥平面PAB,
又∵PB?平面PAB,∴AD⊥PB.
(Ⅱ)解:①以點A為坐標原點,分別以AB,AD,AP為x,y,z軸,建立空間直角坐標系,
則A(0,0,0),B(1,0,0),C(1,1,0),P(0,0,1),
$\overrightarrow{PC}$=(1,1,-1),$\overrightarrow{BC}$=(0,1,0),$\overrightarrow{DC}$=(1,0,0),
設平面PBC的法向量為$\overrightarrow{n}$=(x,y,z),
則$\left\{\begin{array}{l}{x+y-z=0}\\{y=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}$=(1,0,1),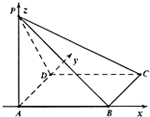
設平面PCD的法向量$\overrightarrow{m}$=(a,b,c),
則$\left\{\begin{array}{l}{a+b-c=0}\\{a=0}\end{array}\right.$,取b=1,得$\overrightarrow{m}$=(0,1,1),
設二面角B-PC-D的大小為θ,
則cosθ=-$\frac{1}{\sqrt{2}×\sqrt{2}}$=-$\frac{1}{2}$,∴θ=120°.
∴二面角B-PC-D的大小為120°.
點評 本題考查異面直線垂直的證明,考查二面角的大小的求法,正確運用向量法是關鍵.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:高中數學 來源: 題型:解答題
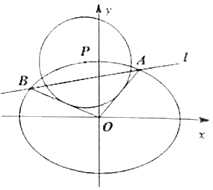 如圖,已知橢圓$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的離心率為$e=\frac{{\sqrt{3}}}{2}$,P為橢圓E上的動點,P到點M(0,2)的距離的最大值為$\frac{2}{3}\sqrt{21}$,直線l交橢圓于A(x1,y1)、B(x2,y2)兩點.
如圖,已知橢圓$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的離心率為$e=\frac{{\sqrt{3}}}{2}$,P為橢圓E上的動點,P到點M(0,2)的距離的最大值為$\frac{2}{3}\sqrt{21}$,直線l交橢圓于A(x1,y1)、B(x2,y2)兩點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$$\overrightarrow{EF}$+$\frac{1}{2}$$\overrightarrow{EG}$+$\frac{1}{2}$$\overrightarrow{EH}$ | B. | $\frac{1}{5}$$\overrightarrow{EF}$+$\frac{1}{5}$$\overrightarrow{EG}$+$\frac{1}{5}$$\overrightarrow{EH}$ | C. | $\frac{1}{4}$$\overrightarrow{EF}$+$\frac{1}{4}$$\overrightarrow{EG}$+$\frac{1}{4}$$\overrightarrow{EH}$ | D. | $\frac{1}{3}$$\overrightarrow{EF}$+$\frac{1}{3}$$\overrightarrow{EG}$+$\frac{1}{3}$$\overrightarrow{EH}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | an=2n-1 | B. | an=(-1)n(1-2n) | C. | an=(-1)n(2n-1) | D. | an(-1)n+1(2n-1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com