
分析 (1)設圓C的方程為x2+y2+Dx+Ey+F=0,建立方程組,即可求圓C的標準方程;
(2)直線l過定點M(3,2).由圓的幾何性質可知,當l⊥CM時,弦長|PQ|最短.
解答 解:(1)設圓C的方程為x2+y2+Dx+Ey+F=0,則$\left\{\begin{array}{l}{-2D+E+F+5=0}\\{5D+F+25=0}\\{E=2D}\end{array}\right.$,
解得D=-4,E=-8,F=-5.(3分)
所以圓C的方程是x2+y2-4x-8y-5=0,
即(x-2)2+(y-4)2=25.(5分)
(2)直線l的方程化為(2x+y-8)+m(x+2y-7)=0.
令$\left\{\begin{array}{l}{2x+y-8=0}\\{x+2y-7=0}\end{array}\right.$,得x=3,y=2,所以直線l過定點M(3,2).(7分)
由圓的幾何性質可知,當l⊥CM時,弦長|PQ|最短.
因為|CM|=$\sqrt{(3-2)^{2}+(2-4)^{2}}$=$\sqrt{5}$
則|PQ|min=2$\sqrt{25-5}$=4$\sqrt{5}$(10分)
點評 本題考查圓的方程,考查圓的幾何性質的運用,屬于中檔題.


 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:選擇題
| A. | (-1,1] | B. | (-2,3] | C. | (-2,-1) | D. | (-2,1-)∪[1,3) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
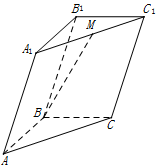
| A. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com