
科目:高中數(shù)學 來源:不詳 題型:單選題
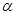 ,
,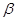 ,
,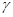 兩兩互相垂直,點
兩兩互相垂直,點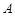 ∈
∈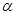 ,點
,點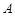 到
到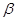 ,
,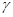 的距離都是
的距離都是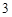 ,點
,點 是
是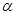 上的動點,滿足
上的動點,滿足 到
到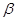 的距離是到
的距離是到 到點
到點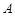 距離的
距離的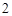 倍,則點
倍,則點 的軌跡上的點到
的軌跡上的點到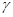 的距離的最小值是
的距離的最小值是A.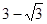 | B.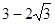 |
C.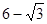 | D.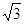 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
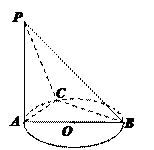 (1)求證:平面PAC⊥平面PBC;
(1)求證:平面PAC⊥平面PBC;查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
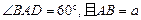 的菱形,ADD``A1和CD D`C1都是正方形.將兩個正方形分別沿AD,CD折起,使D``與D`重合于點D1 .設直線l過點B且垂直于菱形ABCD所在的平面,點E是直線l上的一個動點,且與點D1位于平面ABCD同側(圖2).
的菱形,ADD``A1和CD D`C1都是正方形.將兩個正方形分別沿AD,CD折起,使D``與D`重合于點D1 .設直線l過點B且垂直于菱形ABCD所在的平面,點E是直線l上的一個動點,且與點D1位于平面ABCD同側(圖2).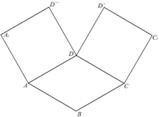
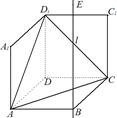
 £q£
£q£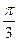 ,求線段BE長的取值范圍;
,求線段BE長的取值范圍;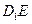 上存在點
上存在點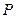 ,使平面
,使平面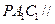 平面
平面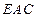 ,求
,求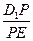 與BE之間滿足的關系式,并證明:當0 < BE < a時,恒有
與BE之間滿足的關系式,并證明:當0 < BE < a時,恒有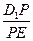 < 1.
< 1.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
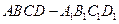 中,
中,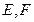 分別是
分別是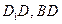 的中點,
的中點,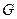 在棱
在棱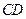 上,且
上,且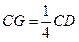 ,H
,H 為
為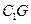 的中點,應用空間向量方法求解下列問題.
的中點,應用空間向量方法求解下列問題.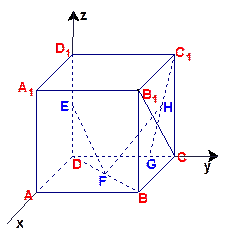
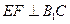 ;
;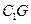 所成的角的余弦;
所成的角的余弦;查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
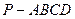 中,點E為PC的中點,則下列命題正確的是( )(正四棱錐即底面為正方
中,點E為PC的中點,則下列命題正確的是( )(正四棱錐即底面為正方 形,四條側棱長相等,頂點在底面上的射影為底面的中心的四棱錐)
形,四條側棱長相等,頂點在底面上的射影為底面的中心的四棱錐)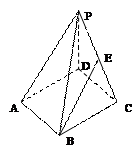
A.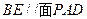 ,且直線BE到面PAD的距離為 ,且直線BE到面PAD的距離為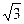 |
B.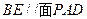 ,且直線BE到面PAD的距離為 ,且直線BE到面PAD的距離為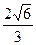 |
C.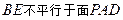 ,且直線BE與面PAD所成的角大于 ,且直線BE與面PAD所成的角大于 |
D.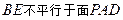 ,且直線BE與面PAD所成的角小于 ,且直線BE與面PAD所成的角小于 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com