
【題目】設函數(shù)![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)若存在正數(shù)![]() ,使得當
,使得當![]() 時,
時,![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]()
【解析】分析:函數(shù)求導得![]() ,討論
,討論![]() ,由導數(shù)的正負求單調區(qū)間即可;
,由導數(shù)的正負求單調區(qū)間即可;
(2)若![]() ,分析函數(shù)可知
,分析函數(shù)可知![]() ,
,![]() 即
即![]() ,設
,設![]() ,
,![]() ,討論
,討論![]() 和
和![]() 兩種情況,知
兩種情況,知![]() 成立,
成立,![]() 時不成立,
時不成立,![]() 時,存在
時,存在![]() ,使得當
,使得當![]() 時,
時,![]() ,
,![]() 可化為
可化為![]() ,即
,即![]() ,設
,設![]() ,分析
,分析![]() 和
和![]() 求解即可.
求解即可.
詳解:(1)![]() .
.
當![]() 時,
時,![]() ,
,![]() 上
上![]() 單調遞增.
單調遞增.
當![]() 時,若
時,若![]() ,則
,則![]() ,若
,若![]() ,則
,則![]() ;所以
;所以![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 上單調遞減.
上單調遞減.
(2)若![]() ,
,![]() 在
在![]() 內單調遞增,當
內單調遞增,當![]() 時,
時,![]() ,所以
,所以![]() ,
,![]() 即
即![]() .
.
設![]() ,
,![]() .
.
若![]() ,
,![]() 時,
時,![]() ,
,![]() 在
在![]() 單調遞增.所以當
單調遞增.所以當![]() 時,
時,![]() ,
,
故存在正數(shù)![]() ,使得當
,使得當![]() 時,
時,![]() .
.
若![]() ,當
,當![]() 時,
時,![]() ,
,![]() 在
在![]() 單調遞減,因為
單調遞減,因為![]() ,所以
,所以![]() .故不存在正數(shù)
.故不存在正數(shù)![]() ,使得當
,使得當![]() 時,
時,![]() .
.
若![]() ,
,![]() 在
在![]() 單調遞減,因為
單調遞減,因為![]() ,所以存在
,所以存在![]() ,使得當
,使得當![]() 時,
時,![]() ,
,![]() 可化為
可化為![]() ,即
,即![]() .
.
設![]() ,
,![]() .
.
若![]() ,則
,則![]() 時,
時,![]() ,
,![]() 在
在![]() 單調遞增,又
單調遞增,又![]() ,所以
,所以![]() 時,
時,![]() .故不存在正數(shù)
.故不存在正數(shù)![]() ,使得當
,使得當![]() 時,
時,![]() .
.
當![]() 時,當
時,當![]() 時,
時,![]() ,
,![]() 在
在![]() 單調遞減,又
單調遞減,又![]() ,所以
,所以![]() .故存在
.故存在![]() ,使得當
,使得當![]() 時,
時,![]() .
.
綜上,實數(shù)![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】以下命題中,正確的命題是:______.
(1)![]() 是奇函數(shù),則
是奇函數(shù),則![]() 的值為0;
的值為0;![]()
(2)若![]() ,則
,則![]() (
(![]() 、
、![]() 且
且![]() 、
、![]() );
);
(3)設集合![]() ,
,![]() ,則
,則![]() ;
;
(4)若![]() 在
在![]() 單調遞增,則
單調遞增,則![]() 的取值集合為
的取值集合為![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 滿足
滿足![]() (
(![]() 為常數(shù)),且
為常數(shù)),且![]() =3.
=3.
(1)求實數(shù)![]() 的值,并求出函數(shù)
的值,并求出函數(shù)![]() 的解析式;
的解析式;
(2)當![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調性,并用定義證明你的結論.
的單調性,并用定義證明你的結論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】分形理論是當今世界十分風靡和活躍的新理論、新學科。其中,把部分與整體以某種方式相似的形體稱為分形。分形是一種具有自相似特性的現(xiàn)象,圖象或者物理過程。標準的自相似分形是數(shù)學上的抽象,迭代生成無限精細的結構。也就是說,在分形中,每一組成部分都在特征上和整體相似,只僅僅是變小了一些而已,謝爾賓斯基三角形就是一種典型的分形,是由波蘭數(shù)學家謝爾賓斯基在1915年提出的,按照如下規(guī)律依次在一個黑色三角形內去掉小三角形則當![]() 時,該黑色三角形內共去掉( )個小三角形
時,該黑色三角形內共去掉( )個小三角形
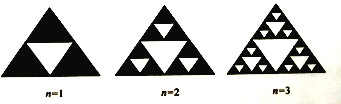
A. 81 B. 121 C. 364 D. 1093
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 過點
過點 ,且兩個焦點的坐標分別為
,且兩個焦點的坐標分別為![]() ,
, ![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
, ![]() ,
, ![]() 為
為![]() 上的三個不同的點,
上的三個不同的點, ![]() 為坐標原點,且
為坐標原點,且![]() ,求證:四邊形
,求證:四邊形![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】近年來,雙十一購物狂歡節(jié)(簡稱“雙11”)活動已成為中國電子商務行業(yè)年度盛事,某網絡商家為制定2018年“雙11”活動營銷策略,調查了2017年“雙11”活動期間每位網購客戶用于網購時間![]() (單位:小時),發(fā)現(xiàn)
(單位:小時),發(fā)現(xiàn)![]() 近似服從正態(tài)分布
近似服從正態(tài)分布![]() .
.
(1)求![]() 的估計值;
的估計值;
(2)該商家隨機抽取參與2017年“雙11”活動的10000名網購客戶,這10000名客戶在2017年“雙11”活動期間,用于網購時間![]() 屬于區(qū)間
屬于區(qū)間![]() 的客戶數(shù)為
的客戶數(shù)為![]() .該商家計劃在2018年“雙11”活動前對這
.該商家計劃在2018年“雙11”活動前對這![]() 名客戶發(fā)送廣告,所發(fā)廣告的費用為每位客戶0.05元.
名客戶發(fā)送廣告,所發(fā)廣告的費用為每位客戶0.05元.
(i)求該商家所發(fā)廣告總費用的平均估計值;
(ii)求使![]() 取最大值時的整數(shù)
取最大值時的整數(shù)![]() 的值.
的值.
附:若隨機變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則
,則![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了解人們對“2019年3月在北京召開的第十三屆全國人民代表大會第二次會議和政協(xié)第十三屆全國委員會第二次會議”的關注度,某部門從年齡在15歲到65歲的人群中隨機調查了100人,并得到如圖所示的年齡頻率分布直方圖,在這100人中關注度非常髙的人數(shù)與年齡的統(tǒng)計結果如右表所示:

年齡 | 關注度非常高的人數(shù) |
| 15 |
| 5 |
| 15 |
| 23 |
| 17 |
(Ⅰ)由頻率分布直方圖,估計這100人年齡的中位數(shù)和平均數(shù);
(Ⅱ)根據(jù)以上統(tǒng)計數(shù)據(jù)填寫下面的![]() 列聯(lián)表,據(jù)此表,能否在犯錯誤的概率不超過
列聯(lián)表,據(jù)此表,能否在犯錯誤的概率不超過![]() 的前提下,認為以45歲為分界點的不同人群對“兩會”的關注度存在差異?
的前提下,認為以45歲為分界點的不同人群對“兩會”的關注度存在差異?
(Ⅲ)按照分層抽樣的方法從年齡在35歲以下的人中任選六人,再從六人中隨機選兩人,求兩人中恰有一人年齡在25歲以下的概率是多少.
45歲以下 | 45歲以上 | 總計 | |
非常髙 | |||
一般 | |||
總計 |
參考數(shù)據(jù):
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著食品安全問題逐漸引起人們的重視,有機、健康的高端綠色蔬菜越來越受到消費者的歡迎,同時生產—運輸—銷售一體化的直銷供應模式,不僅減少了成本,而且減去了蔬菜的二次污染等問題.
(1)在有機蔬菜的種植過程中,有機肥料使用是必不可少的.根據(jù)統(tǒng)計某種有機蔬菜的產量與有機肥料的用量有關系,每個有機蔬菜大棚產量的增加量![]() (百斤)與使用堆漚肥料
(百斤)與使用堆漚肥料![]() (千克)之間對應數(shù)據(jù)如下表
(千克)之間對應數(shù)據(jù)如下表
使用堆漚肥料 | 2 | 4 | 5 | 6 | 8 |
產量的增加量 | 3 | 4 | 4 | 4 | 5 |
依據(jù)表中的數(shù)據(jù),用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;并根據(jù)所求線性回歸方程,估計如果每個有機蔬菜大棚使用堆漚肥料10千克,則每個有機蔬菜大棚產量增加量
;并根據(jù)所求線性回歸方程,估計如果每個有機蔬菜大棚使用堆漚肥料10千克,則每個有機蔬菜大棚產量增加量![]() 是多少百斤?
是多少百斤?
(2)某大棚蔬菜種植基地將采摘的有機蔬菜以每份三斤稱重并保鮮分裝,以每份10元的價格銷售到生鮮超市.“樂購”生鮮超市以每份15元的價格賣給顧客,如果當天前8小時賣不完,則超市通過促銷以每份5元的價格賣給顧客(根據(jù)經驗,當天能夠把剩余的有機蔬菜都低價處理完畢,且處理完畢后,當天不再進貨).該生鮮超市統(tǒng)計了100天有機蔬菜在每天的前8小時內的銷售量(單位:份),制成如下表格(注:![]() ,且
,且![]() );
);
前8小時內的銷售量(單位:份) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
頻數(shù) | 10 | x | 16 | 6 | 15 | 13 | y |
若以100天記錄的頻率作為每日前8小時銷售量發(fā)生的概率,該生鮮超市當天銷售有機蔬菜利潤的期望值為決策依據(jù),當購進17份比購進18份的利潤的期望值大時,求![]() 的取值范圍.
的取值范圍.
附:回歸直線方程為![]() ,其中
,其中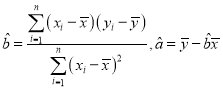 .
.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com