日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

【題目】已知函數，.

（Ⅰ）當時，求的最小值；

（Ⅱ）若有兩個零點，求參數的取值范圍

【答案】（Ⅰ）0；

（Ⅱ）.

【解析】

（Ⅰ）求函數的定義域，再求導，判別導函數的正負可得原函數的單調性，可求得最小值；

（Ⅱ）對a進行分類討論，分別利用其導函數的應用，判別其單調性，求其最值，可得參數a的范圍.

（Ⅰ）,定義域

當時, ,由于 在恒成立

故 在單調遞減, 在單調遞增.

故

（Ⅱ）

當時, 在單調遞減, 在單調遞增,只有一個零點

當時, ,故 在恒成立,

故在單調遞減, 在單調遞增,

故當時, 沒有零點.

當時,令 ,得,

在單調遞減, 在單調遞增. ,

在有兩個零點，

在單調遞減,在 單調遞增,在單調遞減,在單調遞增， ,又

此時有兩個零點，

綜上有兩個零點,則

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

【題目】某種商品價格與該商品日需求量之間的幾組對照數據如下表，經過進一步統計分析，發現y與x具有線性相關關系．

價格x（元/kg）

10

15

20

25

30

日需求量y（kg）

11

10

8

6

5

（1）根據上表給出的數據，求出y與x的線性回歸方程；

（2）利用（1）中的回歸方程，當價格元/kg時，日需求量y的預測值為多少？

（參考公式：線性回歸方程，其中，．）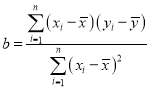

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】經過坐標原點的兩條直線與橢圓：分別相交于點、和點、，其中直線經過的左焦點，直線經過的右焦點.當直線不垂直于坐標軸時，與的斜率乘積為.

（1）求橢圓的方程；

（2）求四邊形面積的最大值.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知是等差數列，滿足， ，數列滿足， ，且是等比數列.

（1）求數列和的通項公式；

（2）求數列的前項和.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】某中學2018年的高考考生人數是2015年高考考生人數的倍，為了更好地對比該校考生的升學情況，統計了該校2015年和2018年的高考情況，得到如圖柱狀圖：

則下列結論正確的是　　

A. 與2015年相比，2018年一本達線人數減少

B. 與2015年相比，2018年二本達線人數增加了倍

C. 2015年與2018年藝體達線人數相同

D. 與2015年相比，2018年不上線的人數有所增加

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】本相同的資料書配給三個班級，要求每班至少一本且至多六本，則不同的分配方法共有_____種．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知拋物線，圓.

（Ⅰ）是拋物線的焦點，是拋物線上的定點，，求拋物線的方程；

（Ⅱ）在（Ⅰ）的條件下，過點的直線與圓相切，設直線交拋物線于，兩點，則在軸上是否存在點使？若存在，求出點的坐標；若不存在，請說明理由.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知數列是各項均為正數的等差數列.

（1）若，且成等比數列，求數列的通項公式；

（2）在（1）的條件下，數列的前和為，設，若對任意的，不等式恒成立，求突數的最小值:

（3）若數列中有兩項可以表示位某個整數的不同次冪，求證:數列中存在無窮多項構成等比數列.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】名學生某次數學考試成績（單位：分）的頻率分布直方圖如圖.

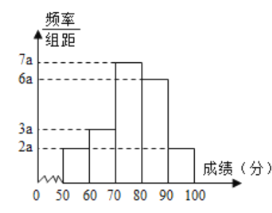
（1）求頻率分布直方圖中的值；

（2）估計總體中成績落在中的學生人數；

（3）根據頻率分布直方圖估計名學生數學考試成績的眾數，中位數.

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 久久性色 | 亚洲v欧美 | 国产精品九九九 | 99色综合| 日韩精品专区 | 国产性×xxx盗摄xxxx | 日韩一区二区在线观看 | 欧美日韩大片在线观看 | 精品九九九 | 免费av在线网站 | 日本一级在线观看 | 国产精品成人在线观看 | 欧美韩一区二区 | 国产精品久久久久久中文字 | 久久六月 | 射久久| 免费精品视频 | 欧美三级一区 | 日韩精品在线免费观看 | a级片视频在线观看 | 国产精品一区二区三 | 国产精品一区二区麻豆 | 欧美日日操 | а_天堂中文最新版地址 | 91久久精品久久国产性色也91 | 日本黄色免费观看 | 天天操天天色天天 | 91精品中文字幕一区二区三区 | 亚洲国产精品麻豆 | 国产在线中文字幕 | 伊人精品视频 | 国产91精品一区二区麻豆网站 | 蜜桃久久av | 波多野结衣在线网址 | 国产成人在线视频观看 | 免费av黄色| 欧美一级一区 | 国产精品一区二区三区四区 | 国产精品久久久久久吹潮 | 国产精品久久久久久亚洲调教 | 精品国产一区二区在线 |