【題目】
本相同的資料書配給三個班級，要求每班至少一本且至多六本，則不同的分配方法共有_____種．
【答案】25.
【解析】
先由題，將
本相同的資料書配給三個班級，要求每班至少一本且至多六本，進行分組，再分別計算每一組的情況，最后求得答案.
先分組，再排序，12本書分三個班級，且每班至少一本且至多六本，可能有
1、5、6；2、4、6；2、5、5；3、3、6；3、4、5；4、4、4共6中情況
當一個班分1本，一個班分5本，一個班分6本，不同的方法有
種；
當一個班分2本，一個班分4本，一個班分6本，不同的方法有種；
當一個班分2本，一個班分5本，一個班分5本，不同的方法有
種；
當一個班分3本，一個班分3本，一個班分6本，不同的方法有種；
當一個班分3本，一個班分4本，一個班分5本，不同的方法有種；
當一個班分4本，一個班分4本，一個班分4本，不同的方法有
種；
所以一共有
故答案為25
科目：高中數學 來源： 題型：
【題目】某紡織廠為了生產一種高端布料，準備從
農場購進一批優質棉花，廠方技術人員從農場存儲的優質棉花中隨機抽取了
處棉花，分別測量了其纖維長度（單位：
）的均值，收集到個樣本數據，并制成如下頻數分布表：
（1）求這個樣本數據的平均數和樣本方差（同一組數據用該區間的中點值作代表）；
（2）將收集到的數據繪制成直方圖可以認為這批棉花的纖維長度服從分布
，其中
.
①利用正態分布，求
；
②紡織廠將農場送來的這批優質棉進行二次檢驗，從中隨機抽取
處測量其纖維均值
，數據如下：
若個樣本中纖維均值
的頻率不低于①中，即可判斷該批優質棉花合格，否則認為農場運送是摻雜了次品，判斷該批棉花不合格.按照此依據判斷農場送來的這批棉花是否為合格的優質棉花，并說明理由.
附：若
，則
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
、
兩個班共有65名學生，為調查他們的引體向上鍛煉情況，通過分層抽樣獲得了部分學生引體向上的測試數據（單位：個），用莖葉圖記錄如下：
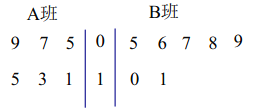
(1)試估計班的學生人數；
(2)從班和班抽出的學生中，各隨機選取一人，班選出的人記為甲，班選出的人記為乙，假設所有學生的測試相對獨立，比較甲、乙兩人的測試數據得到隨機變量
.規定：當甲的測試數據比乙的測試數據低時，記
；當甲的測試數據與乙的測試數據相等時，記
；當甲的測試數據比乙的測試數據高時，記
.求隨機變量的分布列及數學期望.
(3)再從、兩個班中各隨機抽取一名學生，他們引體向上的測試數據分別是10，8（單位：個），這2個新數據與表格中的數據構成的新樣本的平均數記
，表格中數據的平均數記為
，試判斷和的大小.（結論不要求證明）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在長方體
中，
，點E是棱
上的一個動點，若平面
交棱
于點
，給出下列命題：
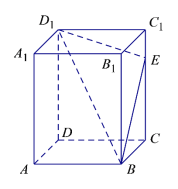
①四棱錐
的體積恒為定值；
②存在點
，使得
平面
；
③對于棱上任意一點，在棱
上均有相應的點
，使得
平面
；
④存在唯一的點，使得截面四邊形
的周長取得最小值.
其中真命題的是____________．（填寫所有正確答案的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓心在x軸上的圓C與直線
切于點
，圓
.
（1）求圓C的標準方程；
（2）已知
，圓P與x軸相交于兩點
（點M在點N的右側），過點M任作一條傾斜角不為0的直線與圓C相交于
兩點.問：是否存在實數a，使得
？若存在，求出實數a的值，若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱柱ABCD﹣A1B1C1D1中，底面四邊形ABCD是矩形，平面DCC1D1⊥平面ABCD.AD=3，CD=DD1=5，∠D1DC=120°，M，N分別是線段AD1，BD的中點.
（1）求證：MN//平面DCC1D1；
（2）求證：MN⊥平面ADC1；
（3）求三棱錐D1﹣ADC1的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】重慶某地區
年至
年農村居民家庭人均純收入
（單位：萬元）的數據如表：
年份 |
|
|
|
|
|
年份代號 |
|
|
|
|
|
純收入 |
|
|
|
|
|
（1）求關于
的線性回歸方程；
（2）利用（1）中的回歸方程，分析年至年該地區農村居民家庭人均純收入的變化情況，并預測該地區
年農村居民家庭人均純收入.
附：回歸直線的斜率和截距的最小二乘法估計公式分別為：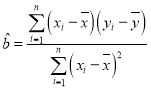
，
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
