Question

6．已知函數f（x）=|lgx|．若a＜b且f（a）=f（b），則a+2b的取值范圍是（　　）

• A． $（2\sqrt{2}，+∞）$
• B． $[2\sqrt{2}，+∞）$
• C． （3，+∞）
• D． [3，+∞）

Answer 1

分析 畫出函數f（x）的圖象，則數形結合可知0＜a＜1，b＞1，且ab=1，再將所求a+2b化為關于a的一元函數，利用函數單調性求函數的值域即可．

解答 解：畫出y=|lgx|的圖象如圖：
∵a＜b，且f（a）=f（b），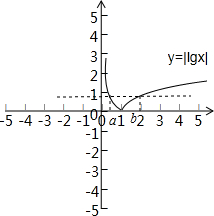
∴|lga|=|lgb|且0＜a＜1，b＞1
∴-lga=lgb
即ab=1
∴y=a+2b=a+$\frac{2}{a}$，a∈（0，1）
∵y=a+$\frac{2}{a}$在（0，1）上為減函數，
∴y＞1+$\frac{2}{1}$=3，
∴a+2b的取值范圍是（3，+∞），
故選：C．

點評 本題主要考查了對數函數的圖象和性質，利用“對勾”函數求函數值域的方法，數形結合的思想方法，轉化化歸的思想方法，屬基礎題．