
| A. | (0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,$\frac{2}{3}$) | C. | ($\frac{2}{3}$,1] | D. | [1,+∞) |
分析 根據分段函數在在R內單調遞減,具有連續性,求出二次函數的對稱軸,對a討論,可求解.
解答 解:由題意:當x<1時,f(x)=x2-4ax+3,對稱軸為x=2a,
要使f(x)在R內單調遞減,函數f(x)=(2-3a)x+1在x≥1必須是減函數,
故得2-3a<0,即a<$\frac{2}{3}$,其最大值為2-3a+1=3-3a,
當2a≥1時,即a$≥\frac{1}{2}$,則f(1)min=1-4a+3=4-4a,
需滿足:3-3a≤4-4a,
解得:a≤1,
故而:$\frac{1}{2}≤a<\frac{3}{2}$.
故選B.
點評 本題考查了分段函數的單調性的綜合運用能力和計算能力.屬于中檔題.


科目:高中數學 來源: 題型:填空題
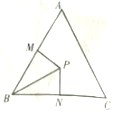 如圖,△ABC三個內角A,B,C所對的邊分別為a,b,c,已知C=$\frac{π}{3}$,$\frac{a}{b}$=$\frac{cosB}{cosA}$,在△ABC內取一點P,使得PB=3,過點P分別作直線BA,BC的垂線PM,PN,垂足分別是M,N,則|PM|+|PN|的最大值為3.
如圖,△ABC三個內角A,B,C所對的邊分別為a,b,c,已知C=$\frac{π}{3}$,$\frac{a}{b}$=$\frac{cosB}{cosA}$,在△ABC內取一點P,使得PB=3,過點P分別作直線BA,BC的垂線PM,PN,垂足分別是M,N,則|PM|+|PN|的最大值為3.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com