
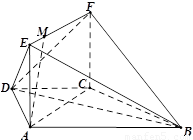
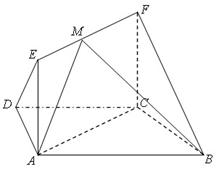
如圖,在梯形 中,
中,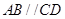 ,
,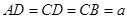 ,
,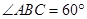 ,平面
,平面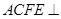 平面
平面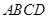 ,四邊形
,四邊形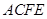 是矩形,
是矩形, ,點
,點 在線段EF上.
在線段EF上.
(1)求異面直線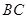 與
與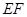 所成的角;
所成的角;
(2)求二面角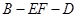 的余弦值.
的余弦值.
(1)900 ;(2)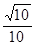 .
.
【解析】
試題分析:(1)要求異面直線所成的角,可轉化為求其中一條直線與另外一直線的平行線所成的角的大小;(2)法一:利用幾何法,求二面角需要先找出二面角的平面角,再在平面角所在的三角形中根據邊長由余弦定理求平面角的余弦值,即二面角的余弦值;法二:利用向量法,首先建立直角坐標系,寫出所需各點的坐標以及向量的坐標,再設出二面角所在兩個面的法向量,利用向量垂直求出法向量的一組值,求兩個法向量的夾角的余弦值,從而得二面角的余弦值.
試題解析:(1)在梯形ABCD中,∵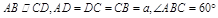 ,
,
∴四邊形ABCD是等腰梯形, 且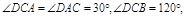
∴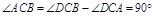 ,∴
,∴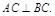
又∵平面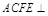 平面ABCD,交線為AC,∴
平面ABCD,交線為AC,∴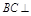 平面ACFE. ∴
平面ACFE. ∴ 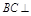 平面FE.
平面FE.
∴異面直線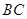 與
與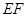 所成的角為900
7分
所成的角為900
7分
(2)方法一;(幾何法)取EF中點G,EB中點H,連結DG、GH、DH,
∵容易證得DE=DF,∴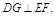
∵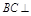 平面ACFE,∴
平面ACFE,∴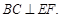 又∵
又∵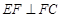 ,∴
,∴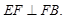
又∵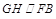 ,∴
,∴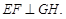
∴ 是二面角B—EF—D的平面角.
是二面角B—EF—D的平面角.
在△BDE中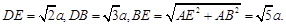
∴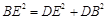 ∴
∴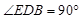 ,
,
∴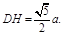 又
又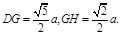 ∴在△DGH中,
∴在△DGH中,
由余弦定理得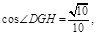 即二面角B—EF—D的平面角余弦值為
即二面角B—EF—D的平面角余弦值為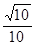 .
15分
.
15分
方法二;(向量法)以C為坐標原點,建立如圖所示的直角坐標系,
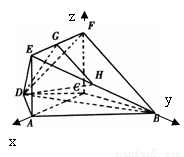
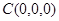 ,
,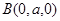 ,
,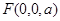 ,
,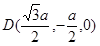 ,
,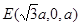
所以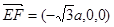 ,
,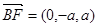 ,
,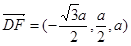
分別設平面BEF與平面DEF的法向量為
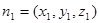 ,
,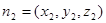
所以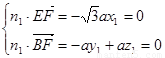 ,令
,令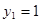 ,則
,則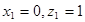
又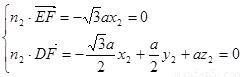 ,顯然
,顯然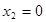 ,令
,令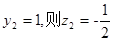
所以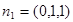 ,
,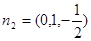 ,設二面角的平面角為
,設二面角的平面角為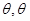 為銳角
為銳角
所以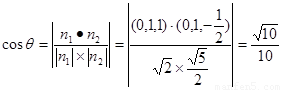 15分
15分
考點:1、異面直線所成的角;2、二面角;3、面面垂直的性質定理;4、余弦定理.


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源:2012-2013學年江蘇省高三下學期期中考試數學試卷(解析版) 題型:解答題
[選修4 - 1:幾何證明選講](本小題滿分10分)
如圖,在梯形 中,
中,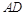 ∥BC,點
∥BC,點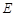 ,
, 分別在邊
分別在邊 ,
, 上,設
上,設 與
與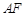 相交于點
相交于點 ,若
,若 ,
, ,
, ,
,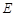 四點共圓,求證:
四點共圓,求證: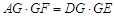 .
. 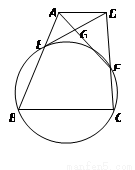
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三第一次統考理科數學 題型:解答題
如圖,在梯形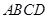 中,
中,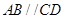 ,
,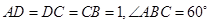 ,四邊形
,四邊形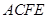 為矩
為矩
形,平面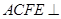 平面
平面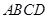 ,
,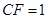 .
.
(I)求證: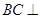 平面
平面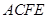 ;
;
(II)點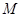 在線段
在線段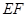 上運動,設平面
上運動,設平面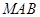 與平面
與平面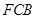 所成二面角的平面角為
所成二面角的平面角為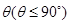 ,試求
,試求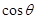
的取值范圍.

查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三第七次月考理科數學 題型:解答題
如圖,在梯形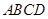 中,
中,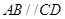 ,
,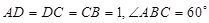 ,四邊形
,四邊形
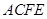 為矩形,平面
為矩形,平面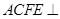 平面
平面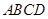 ,
,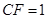 .
.
(I)求證: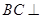 平面
平面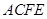 ;
;
(II)點 在線段
在線段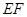 上運動,設平面
上運動,設平面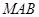 與平面
與平面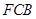 所成二面角的平面角為
所成二面角的平面角為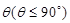 ,
,
試求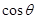 的取值范圍.
的取值范圍.
查看答案和解析>>
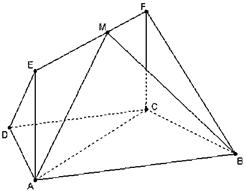
科目:高中數學 來源:2011-2012學年山東省煙臺市高三下學期3月診斷性測試理科數學 題型:解答題
(本題滿分12分)
如圖,在梯形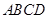 中,
中,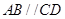 ,
,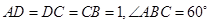 ,四邊形
,四邊形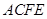 為矩形,平面
為矩形,平面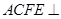 平面
平面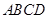 ,
,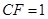 .
.
(1)求證: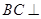 平面
平面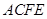 ;
;
(2)點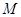 在線段
在線段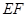 上運動,設平面
上運動,設平面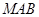 與平面
與平面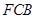 所成二面角的平面角為
所成二面角的平面角為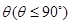 ,試求
,試求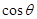 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年安徽省高三上學期期末考試理科數學 題型:解答題
如圖,在梯形 中
中 ‖
‖ ,平面
,平面 平面
平面 ,四邊形
,四邊形 是矩形,
是矩形, ,點
,點 在線段
在線段 上.
上.
(Ⅰ)求證: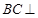 平面
平面 ;
;
(Ⅱ)當 為何值時,
為何值時, ‖平面
‖平面 ?證明你的結論;
?證明你的結論;
(Ⅲ)求二面角 的大小.
的大小.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com