
分析 把“1”換成4a+b,整理后積為定值,然后用基本不等式求最小值
解答 解:∵ab>0,且a+4b=1,
∴$\frac{1}{a}+\frac{1}{b}$=($\frac{1}{a}+\frac{1}{b}$)(a+4b)=1+4+$\frac{4b}{a}$+$\frac{a}{b}$≥5+2$\sqrt{\frac{4b}{a}•\frac{a}{b}}$=9,當且僅當a=$\frac{1}{3}$,b=$\frac{1}{6}$時取等號,
∴$\frac{1}{a}+\frac{1}{b}$的最小值為9,
故答案為:9.
點評 本題考查了基本不等式在求最值中的應用,解決本題的關鍵是“1”的代換.


科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
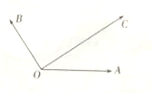 如圖所示,平面內有三個向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,其中$\overrightarrow{OA}$與$\overrightarrow{OC}$的夾角為30°,$\overrightarrow{OB}$與$\overrightarrow{OC}$的夾角為90°,且|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OC}$|=2$\sqrt{3}$,若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,(λ,μ∈R)則( )
如圖所示,平面內有三個向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,其中$\overrightarrow{OA}$與$\overrightarrow{OC}$的夾角為30°,$\overrightarrow{OB}$與$\overrightarrow{OC}$的夾角為90°,且|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2,|$\overrightarrow{OC}$|=2$\sqrt{3}$,若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,(λ,μ∈R)則( )| A. | λ=4,μ=2 | B. | λ=4,μ=1 | C. | λ=2,μ=1 | D. | λ=2,μ=2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com