
【題目】已知函數![]() ,
,![]() .
.
(1)求函數![]() 的極值;
的極值;
(2)對![]() ,不等式
,不等式![]() 都成立,求整數k的最大值;
都成立,求整數k的最大值;
 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:高中數學 來源: 題型:
【題目】若定義在R上的函數![]() 滿足:對于任意實數x、y,總有
滿足:對于任意實數x、y,總有![]() 恒成立,我們稱
恒成立,我們稱![]() 為“類余弦型”函數.
為“類余弦型”函數.
![]() 已知
已知![]() 為“類余弦型”函數,且
為“類余弦型”函數,且![]() ,求
,求![]() 和
和![]() 的值;
的值;
![]() 在
在![]() 的條件下,定義數列
的條件下,定義數列![]() 2,3,
2,3,![]() 求
求![]() 的值.
的值.
![]() 若
若![]() 為“類余弦型”函數,且對于任意非零實數t,總有
為“類余弦型”函數,且對于任意非零實數t,總有![]() ,證明:函數
,證明:函數![]() 為偶函數,設有理數
為偶函數,設有理數![]() ,
,![]() 滿足
滿足![]() ,判斷
,判斷![]() 和
和![]() 的大小關系,并證明你的結論.
的大小關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面內任意一點![]() 到兩定點
到兩定點![]() 、
、![]() 的距離之和為
的距離之和為![]() .
.
(1)若點![]() 是第二象限內的一點且滿足
是第二象限內的一點且滿足![]() ,求點
,求點![]() 的坐標;
的坐標;
(2)設平面內有關于原點對稱的兩定點![]() ,判別
,判別![]() 是否有最大值和最小值,請說明理由?
是否有最大值和最小值,請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正四棱柱ABCD﹣A1B1C1D1中,O是BD的中點,E是棱CC1上任意一點.
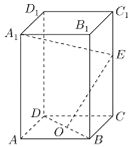
(1)證明:BD⊥A1E;
(2)如果AB=2,![]() ,OE⊥A1E,求AA1的長.
,OE⊥A1E,求AA1的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 與拋物線
與拋物線![]() :
:![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() 的面積為16(
的面積為16(![]() 為坐標原點).
為坐標原點).
(1)求![]() 的方程.
的方程.
(2)直線![]() 經過
經過![]() 的焦點
的焦點![]() 且
且![]() 不與
不與![]() 軸垂直,
軸垂直,![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,若線段
兩點,若線段![]() 的垂直平分線與
的垂直平分線與![]() 軸交于點
軸交于點![]() ,試問在
,試問在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() 為定值?若存在,求該定值及
為定值?若存在,求該定值及![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在①函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度得到
個單位長度得到![]() 的圖象,
的圖象,![]() 圖象關于原點對稱;②向量
圖象關于原點對稱;②向量![]() ,
,![]() ;③函數
;③函數![]()
![]() 這三個條件中任選一個,補充在下面問題中,并解答.已知_________,函數
這三個條件中任選一個,補充在下面問題中,并解答.已知_________,函數![]() 的圖象相鄰兩條對稱軸之間的距離為
的圖象相鄰兩條對稱軸之間的距離為![]() .
.
(1)若![]() 且
且![]() ,求
,求![]() 的值;
的值;
(2)求函數![]() 在
在![]() 上的單調遞減區間.
上的單調遞減區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用一個長為![]() ,寬為
,寬為![]() 的矩形鐵皮(如圖1)制作成一個直角圓形彎管(如圖3):先在矩形的中間畫一條曲線,并沿曲線剪開,將所得的兩部分分別卷成體積相等的斜截圓柱狀(如圖2),然后將其中一個適當翻轉拼接成直角圓形彎管(如圖3)(不計拼接損耗部分),并使得直角圓形彎管的體積最大;
的矩形鐵皮(如圖1)制作成一個直角圓形彎管(如圖3):先在矩形的中間畫一條曲線,并沿曲線剪開,將所得的兩部分分別卷成體積相等的斜截圓柱狀(如圖2),然后將其中一個適當翻轉拼接成直角圓形彎管(如圖3)(不計拼接損耗部分),并使得直角圓形彎管的體積最大;
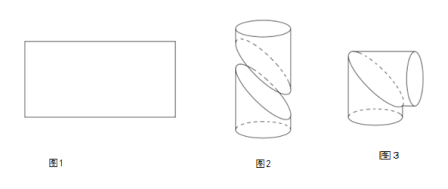
(1)求直角圓形彎管(圖3)的體積;
(2)求斜截面橢圓的焦距;
(3)在相應的圖1中建立適當的坐標系,使所畫的曲線的方程為![]() ,求出方程并畫出大致圖像;
,求出方程并畫出大致圖像;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com