
| A. | f(x)=x3-x2+x | B. | f(x)=-2x+sinx | C. | f(x)=ex-e-x | D. | f(x)=1+xlnx |
分析 若函數y=f(x)的圖象上存在兩點,使得函數的圖象在這兩點處的切線互相垂直,則函數y=f(x)的導函數上存在兩點,使這點的導函數值乘積為-1,進而可得答案.
解答 解:函數y=f(x)的圖象上存在兩點,使得函數的圖象在這兩點處的切線互相垂直,
則函數y=f(x)的導函數上存在兩點,使這點的導函數值乘積為-1,
當f(x)=x3-x2+x時,f′(x)=3x2-2x+1≥$\frac{2}{3}$,不滿足條件;
當f(x)=-2x+sinx時,f′(x)=-2+cosx<0恒成立,不滿足條件;
當f(x)=ex-e-x時,f′(x)=ex+e-x≥2,不滿足條件;
當f(x)=1+xlnx時,f′(x)=1+lnx∈R,滿足條件.
故選:D.
點評 本題考查的知識點是利用導數研究曲線上某點切線方程,轉化思想,難度中檔.


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:高中數學 來源: 題型:選擇題
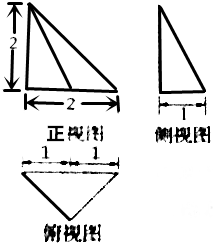
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | k<-1 | B. | k≤-1 | C. | k>-1 | D. | k≥-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
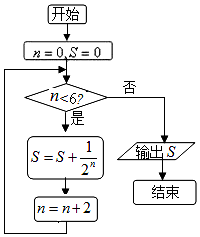
| A. | $\frac{5}{4}$ | B. | $\frac{21}{16}$ | C. | $\frac{63}{32}$ | D. | $\frac{85}{64}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com