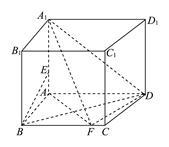
(本小題滿分14分)已知在直四棱柱ABCDA
1B
1C
1D
1中,底面ABCD為直角梯形,且滿足AD⊥AB,BC∥AD,AD=16,AB=8,BB
1=8,E,F(xiàn)分別是線段A
1A,BC上的點.
(1) 若A
1E=5,BF=10,求證:BE∥平面A
1FD.
(2) 若BD⊥A
1F,求三棱錐A
1AB
1F的體積.
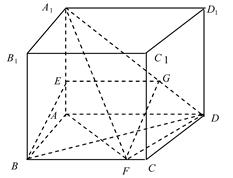
(1) 過E作EG∥AD交A
1D于G,連接GF.
∵=,∴=,∴EG=10=BF.
∵BF∥AD,EG∥AD,∴BF∥EG.
∴四邊形BFGE是平行四邊形.
∴BE∥FG.(4分)
又FG?平面A
1FD,BE?平面A
1FD,
∴BE∥平面A
1FD.(6分)
(2) ∵在直四棱柱ABCDA
1B
1C
1D
1中,A
1A⊥平面ABCD,BD?平面ABCD,∴A
1A⊥BD.
由已知,BD⊥A
1F,AA
1∩A
1F=A
1,
∴BD⊥平面A
1AF.
∴BD⊥AF.(8分)
∵梯形ABCD為直角梯形,且滿足AD⊥AB,BC∥AD,
∴在Rt△BAD中,tan∠ABD==2.
在Rt△ABF中,tan∠BAF==.
∵BD⊥AF,∴∠ABD+∠BAF

=,
∴=,BF=4.(10分)
∵在直四棱柱ABCDA
1B
1C
1D
1中,A
1A⊥平面ABCD,∴平面AA
1B
1B⊥平面ABCD,
又平面ABCD∩平面AA
1B
1B=AB,∠ABF=90°,
∴FB⊥平面AA
1B
1B,即BF為三棱錐FA
1B
1A的高.(12分)
∵∠AA
1B
1=90°,AA
1=BB
1=8,A
1B
1=AB=8,
∴S△AA
1B
1=32.
∴V三棱錐A
1AB
1F=V三棱錐FA
1B
1A=×S△AA
1B
1×BF=.(14分)
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖,在棱長為

的正方體

中,異面直線

與

所成的角等于( )

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在四棱錐
P—ABCD中,
PA⊥底面
ABCD,底面為直角梯形,
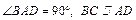
,且
PA=AB=BC=1,
AD=2.
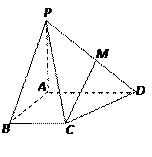
(Ⅰ)設(shè)
M為
PD的中點,求證:
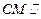
平面
PAB;
(Ⅱ)求側(cè)面
PAB與側(cè)面
PCD所成二面角的平面角的正切值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在正方形

中,
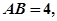
沿對角線
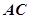
將正方形
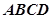
折成一個直二面角
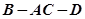
,則點
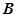
到直線
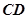
的距離為(
)
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
一條直線若同時平行于兩個相交平面,則這條直線與這兩個平面的交線的位置關(guān)系是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖,四面體
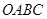
的三條棱
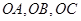
兩兩垂直,
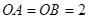
,
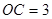
,
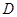
為四面體
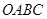
外一點.給出下列命題.
①不存在點
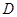
,使四面體
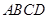
有三個面是直角三角形
②不存在點
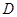
,使四面體
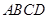
是正三棱錐
③存在點
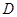
,使
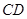
與
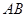
垂直并且相等
④存在無數(shù)個點
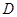
,使點
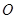
在四面體
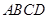
的外接球面上
其中真命題的序號是
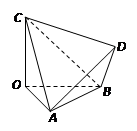
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
平面上有四點,連結(jié)其中的兩點的一切直線中的任何兩條直線不重合、不平行、不垂直,從每一點出發(fā),向其他三點作成的一切直線作垂線,則這些垂線的交點個數(shù)最多為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
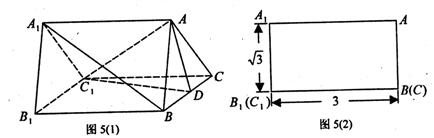
.如圖5(1)是一個水平放置的正三棱柱ABC—A
1B
1C
1,D是棱BC的中點,正三棱柱的正(主)視圖如圖5(2)。
(1)求正三棱柱ABC—A
1B
1
C
1的體積;
(2)證明:A
1B//平面ADC
1;
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖1,在正三角形ABC中,D、E、F分別為各邊的中點,G、H、I、J分別為AF、AD、BE、DE的中點.將△ABC沿DE、EF、DF折成三棱錐以后,GH與IJ所成角的度數(shù)為( )
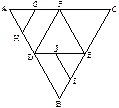
A.90° B.60° C.45° D.0°
查看答案和解析>>



 =,
=,

 ,且PA=AB=BC=1,AD=2.
,且PA=AB=BC=1,AD=2.
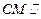 平面PAB;
平面PAB;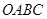 的三條棱
的三條棱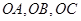 兩兩垂直,
兩兩垂直,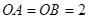 ,
,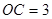 ,
,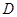 為四面體
為四面體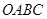 外一點.給出下列命題.
外一點.給出下列命題.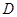 ,使四面體
,使四面體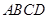 有三個面是直角三角形
有三個面是直角三角形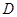 ,使四面體
,使四面體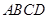 是正三棱錐
是正三棱錐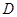 ,使
,使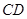 與
與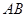 垂直并且相等
垂直并且相等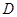 ,使點
,使點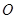 在四面體
在四面體 的外接球面上
的外接球面上
 C1的體積;
C1的體積;