
分析 由約束條件作出可行域,結合題意求出m,利用線性規劃知識求得p,再由兩點求斜率求出q,則答案可求.
解答 解:由約束條件作出可行域如圖,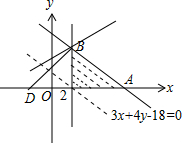
∵平面區域Ω夾在兩條斜率為-$\frac{3}{4}$的平行直線之間,且兩條平行直線間的最短距離為m,
則m=$\frac{|3×2-18|}{5}$=$\frac{12}{5}$.
令z=mx-y=$\frac{12}{5}$x-y,則y=$\frac{12}{5}$x-z,
由圖可知,當直線y=$\frac{12}{5}$x-z過B(2,3)時,直線在y軸上的截距最大,z有最小值為p=$\frac{9}{5}$,
$\frac{y}{x+m}$=$\frac{y}{x+\frac{12}{5}}$的幾何意義為可行域內的動點與定點D(-$\frac{12}{5}$,0)連線的斜率,
其最大值q=$\frac{3}{2+\frac{12}{5}}=\frac{15}{22}$.
∴pq=$\frac{9}{5}×\frac{15}{22}=\frac{27}{22}$.
故答案為:$\frac{27}{22}$.
點評 本題考查簡單的線性規劃,考查了數形結合的解題思想方法和數學轉化思想方法,是中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
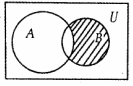
| A. | {x|-2≤x<4} | B. | {x|x≤2或x≥4} | C. | {x|-2≤x≤-1} | D. | {x|-1≤x≤2} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com