
如圖1,A,D分別是矩形A1BCD1上的點,AB=2AA1=2AD=2,DC=2DD1,把四邊形A1ADD1沿AD折疊,使其與平面ABCD垂直,如圖2所示,連接A1B,D1C得幾何體ABA1DCD1.
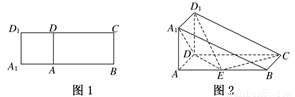
(1)當點E在棱AB上移動時,證明:D1E⊥A1D;
(2)在棱AB上是否存在點E,使二面角D1ECD的平面角為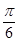 ?若存在,求出AE的長;若不存在,請說明理由.
?若存在,求出AE的長;若不存在,請說明理由.
(1)見解析 (2)存在,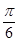
【解析】解:(1)證明,如圖,以點D為坐標原點,DA,DC,DD1所在直線為x軸,y軸,z軸建立空間直角坐標系Dxyz,
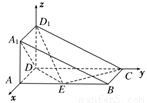
則D(0,0,0),A(1,0,0),C(0,2,0),A1(1,0,1),D1(0,0,1).設E(1,t,0),
則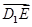 =(1,t,-1),
=(1,t,-1),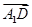 =(-1,0,-1),
=(-1,0,-1),
∴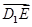 ·
·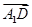 =1×(-1)+t×0+(-1)×(-1)=0,
=1×(-1)+t×0+(-1)×(-1)=0,
∴D1E⊥A1D.
(2)假設存在符合條件的點E.設平面D1EC的法向量為n=(x,y,z),
由(1)知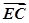 =(-1,2-t,0),
=(-1,2-t,0),
則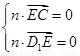 得
得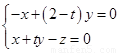
令y=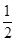 ,則x=1-
,則x=1-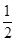 t,z=1,
t,z=1,
∴n=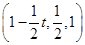 是平面D1EC的一個法向量,
是平面D1EC的一個法向量,
顯然平面ECD的一個法向量為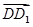 =(0,0,1),
=(0,0,1),
則cos〈n,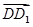 〉=
〉=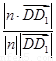
=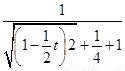 =cos
=cos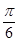 ,
,
解得t=2-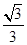 (0≤t≤2).
(0≤t≤2).
故存在點E,
當AE=2-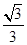 時,二面角D1ECD的平面角為
時,二面角D1ECD的平面角為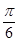 .
.


 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數(shù)學 來源: 題型:
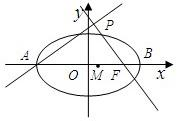 如圖,點A,B分別是橢圓
如圖,點A,B分別是橢圓| x2 |
| 36 |
| y2 |
| 20 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 如圖,點A、B分別是橢圓
如圖,點A、B分別是橢圓| x2 |
| 36 |
| y2 |
| 20 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
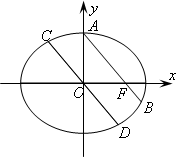 如圖,點A,F(xiàn)分別是橢圓
如圖,點A,F(xiàn)分別是橢圓| x2 |
| a2 |
| y2 |
| b2 |
| CD |
| AB |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源:2013屆海南省高二上學期期末文科數(shù)學試題(解析版) 題型:解答題
(本小題滿分12分)如圖,點A,B分別是橢圓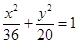 的長軸的左右端點,點F為橢圓的右焦點,直線PF的方程為:
的長軸的左右端點,點F為橢圓的右焦點,直線PF的方程為: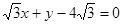 且
且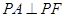 .
.
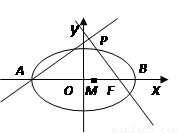
(1)求直線AP的方程;
(2)設點M是橢圓長軸AB上一點,點M到直線AP的距離等于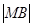 ,求橢圓上的點到點M的距離d的最小值.
,求橢圓上的點到點M的距離d的最小值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com