
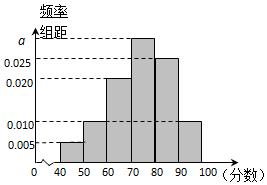
 某校從高二年級學生中隨機抽取40名學生,將他們的期中考試數學成績(滿分100分,成績均為不低于40分的整數)分成六段:[40,50),[50,60),…,[90,100]后得到如圖的頻率分布直方圖.
某校從高二年級學生中隨機抽取40名學生,將他們的期中考試數學成績(滿分100分,成績均為不低于40分的整數)分成六段:[40,50),[50,60),…,[90,100]后得到如圖的頻率分布直方圖.分析 (1)根據頻率和為1,列出方程求出a的值;
(2)根據頻率分布直方圖,計算成績不低于60分的頻率與頻數即可;
(3)計算成績在[50,60)和[90,100]內的人數,利用列舉法求出基本事件數,計算對應的概率值.
解答 解:(1)由于圖中所有小矩形的面積之和等于1,
所以10×(0.005+0.01+0.02+a+0.025+0.01)=1; …(2分)
解得a=0.03; …(3分)
(2)根據頻率分布直方圖,成績不低于60分的頻率為
1-10×(0.05+0.01)=0.85,…(4分)
由于該校高二年級共有學生640人,利用樣本估計總體的思想,
可估計該校高二年級數學成績不低于60分的人數約為
640×0.85=544(人); …(6分)
(如果沒有:“利用樣本估計總體的思想,可估計”則扣1分)
(3)成績在[50,60)分數段內的人數為
40×0.05=2(人),…(7分)
成績在[90,100]分數段內的人數為
40×0.1=4(人),…(8分)
若從這6名學生中隨機抽取2人,則總的取法有
$C_6^2=15$;…(9分)
如果兩名學生的數學成績都在[40,50)分數段內或都在[90,100]分數段內,
那么這兩名學生的數學成績之差的絕對值一定不大于10;
如果一個成績在[40,50)分數段內,另一個成績在[90,100]分數段內,
那么這兩名學生的數學成績之差的絕對值一定大于10;…(10分)
則所取兩名學生的數學成績之差的絕對值大于10分的取法數為
$C_2^1•C_4^1=8$;…(11分)
故所求概率為
$P(M)=\frac{8}{15}$. …(12分)
點評 本題考查了頻率分布直方圖以及用列舉法求古典概型的概率問題,是綜合性題目.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題P使用了邏輯聯結詞“或”,是假命題 | |
| B. | 命題P使用了邏輯聯結詞“且”,是假命題 | |
| C. | 命題P使用了邏輯聯結詞“非”,是假命題 | |
| D. | 命題P使用了邏輯聯結詞“或”,是真命題 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
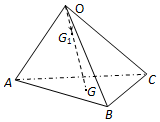
| A. | $\overrightarrow{O{G}_{1}}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G}_{1}}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{3}{4}$$\overrightarrow{OB}$+$\frac{3}{4}$$\overrightarrow{OC}$ | D. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{9}$$\overrightarrow{OA}$+$\frac{1}{9}$$\overrightarrow{OB}$+$\frac{1}{9}$$\overrightarrow{OC}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
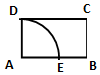 如圖,四邊形ABCD為距形,AB=$\sqrt{3}$,BC=1,以A為圓心,AD為半徑畫圓,交線段AB于E,在圓弧DE上任取一點P,則直線AP與線段BC有公共點的概率為( )
如圖,四邊形ABCD為距形,AB=$\sqrt{3}$,BC=1,以A為圓心,AD為半徑畫圓,交線段AB于E,在圓弧DE上任取一點P,則直線AP與線段BC有公共點的概率為( )| A. | $\frac{\sqrt{3}π}{12}$ | B. | $\frac{12-\sqrt{3}π}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com