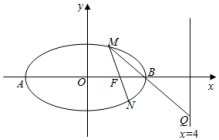
【題目】在平面直角坐標系xOy中，橢圓C的中心在坐標原點O，其右焦點為
，且點
在橢圓C上．
求橢圓C的方程；
設橢圓的左、右頂點分別為A、B，M是橢圓上異于A，B的任意一點，直線MF交橢圓C于另一點N，直線MB交直線
于Q點，求證：A，N，Q三點在同一條直線上．
狀元及第系列答案
同步奧數系列答案科目：高中數學 來源： 題型：
【題目】下表列出了10名5至8歲兒童的體重x(單位kg)(這是容易測得的)和體積y(單位dm3)(這是難以測得的)，繪制散點圖發現，可用線性回歸模型擬合y與x的關系：
體重x | 17.00 10.50 13.80 15.70 11.90 10.20 15.00 17.80 16.00 12.10 |
體積y | 16. 70 10.40 13.50 15.70 11.60 10.00 14.50 17.50 15.40 11.70 |
(1)求y關于x的線性回歸方程
(系數精確到0.01)；
(2)某5歲兒童的體重為13.00kg，估測此兒童的體積．
附注：參考數據：
，
，
，
，
，
，137×14=1918.00．
參考公式：回歸方程中斜率和截距的最小二乘法估計公式分別為：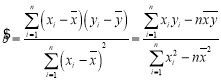
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
的離心率為
，左、右頂點分別為A，B，點M是橢圓C上異于A，B的一點，直線AM與y軸交于點P．
（Ⅰ）若點P在橢圓C的內部，求直線AM的斜率的取值范圍；
（Ⅱ）設橢圓C的右焦點為F，點Q在y軸上，且∠PFQ=90°，求證：AQ∥BM．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
，
）的圖象與
軸交點的橫坐標構成一個公差為
的等差數列，把函數
的圖象沿軸向左平移
個單位，縱坐標擴大到原來的2倍得到函數
的圖象，則下列關于函數的命題中正確的是（ ）
A.函數是奇函數B.的圖象關于直線
對稱
C.在
上是增函數D.當
時，函數的值域是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動點
到直線
的距離比到定點
的距離大1.
（1）求動點的軌跡
的方程.
（2）若
為直線
上一動點，過點作曲線的兩條切線
，
，切點為
，
，
為
的中點.
①求證：
軸；
②直線是否恒過一定點？若是，求出這個定點的坐標；若不是，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正方體
，過對角線
作平面
交棱
于點E，交棱
于點F，則：
①平面分正方體所得兩部分的體積相等；
②四邊形
一定是平行四邊形；
③平面與平面
不可能垂直；
④四邊形的面積有最大值.
其中所有正確結論的序號為（ ）
A.①④B.②③C.①②④D.①②③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，點A(0,3)，直線l：y＝2x－4，設圓C的半徑為1，圓心在l上．若圓C上存在點M，使MA＝2MO，則圓心C的橫坐標a的取值范圍是（ ）
A.
B.[0,1]
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
(a為常數)有兩個極值點．
(1)求實數a的取值范圍；
(2)設f(x)的兩個極值點分別為x1，x2，若不等式f(x1)＋f(x2)＜λ(x1＋x2)恒成立，求λ的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
