【題目】為了打擊海盜犯罪，甲、乙、丙三國海軍進行聯合軍事演習，分別派出一艘軍艦A，B，C.演習要求：任何時刻軍艦A、B、C均不得在同一條直線上.
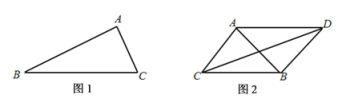
（1）如圖1，若演習過程中，A、B間的距離始終保持
，B，C間的距離始終保持
，求
的最大值.
（2）如圖2，若演習過程中，A，C間的距離始終保持
，B、C間的距離始終保持
.且當變化時，模擬海盜船D始終保持：到B的距離與A、B間的距離相等，
，與C在直線AB的兩側，求C與D間的最大距離.
【答案】（1）
（2）C與D間的最大距離為
【解析】
（1）由正弦定理求出
的取值范圍后可得
的最大值；
（2））以C為坐標原點，CB所在直線為x軸，建立如圖所示的平面直角坐標系xOy，
則
，由
，得A在圓
上.設
，得
，由到
及
，與C在直線AB的兩側，可
，從而得
點坐標，代入點軌跡方程可得
點軌跡方程，知軌跡為圓，從而由點與圓的位置關系可得最大距離．
因為任何時刻軍艦A，B，C均不得在同一條直線上，所以構成
，記角A，B，C的對邊分別為a，b，c.
（1）在中，
，
，
由正弦定理
，得
所以
.
又因為
.所以
答：∠ACB的最大值是.
（2）以C為坐標原點，CB所在直線為x軸，建立如圖所示的平面直角坐標系xOy，
則
因為，所以A在圓上.
設
，則
.
因為D始終保持：到B的距離與A，B間的距離相等，
且，與C在直線AB的兩側，
所以
，所以
.
代入方程中，得
，
所以D在以點
為圓心1為半徑的圓上，
故
.
答：C與D間的最大距離為.
小學奪冠AB卷系列答案科目：高中數學 來源： 題型：
【題目】如圖，由直三棱柱
和四棱錐
構成的幾何體中， 
，平面
平面
．
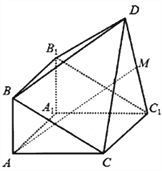
（Ⅰ）求證： 
；
（Ⅱ）在線段
上是否存在點
，使直線
與平面
所成的角為
？若存在，求
的值，若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示多面體中，AD⊥平面PDC，四邊形ABCD為平行四邊形，點E，F分別為AD，BP的中點，AD＝3，AP＝3
，PC
．
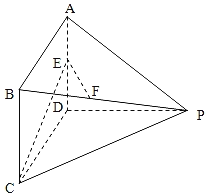
（1）求證：EF//平面PDC；
（2）若∠CDP＝120°，求二面角E﹣CP﹣D的平面角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合
，從P中任取2個元素，分別記為a，b.
（1）若
，隨機變量X表示ab被3除的余數，求
的概率；
（2）若
（
且
），隨機變量Y表示
被5除的余數，求Y的概率分布及數學期望
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，短軸的一個端點到右焦點的距離為2．
（1）求橢圓
的方程；
（2）設
分別為橢圓的左、右頂點，如圖，過點分別作直線
與
，設直線交橢圓于另一點
交橢圓于另一點
，分別過
和作橢圓的兩條切線，且兩條切線交于點
，分別過
和
作橢圓的兩條切線，且兩條切線交于點
．證明：點
在直線
上．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
