
【題目】若數列![]() 滿足:對于
滿足:對于![]() ,都有
,都有![]() (
(![]() 為常數),則稱數列
為常數),則稱數列![]() 是公差為
是公差為![]() 的“隔項等差”數列.
的“隔項等差”數列.
(Ⅰ)若![]() ,
,![]() 是公差為8的“隔項等差”數列,求
是公差為8的“隔項等差”數列,求![]() 的前
的前![]() 項之和;
項之和;
(Ⅱ)設數列![]() 滿足:
滿足:![]() ,對于
,對于![]() ,都有
,都有![]() .
.
①求證:數列![]() 為“隔項等差”數列,并求其通項公式;
為“隔項等差”數列,并求其通項公式;
②設數列![]() 的前
的前![]() 項和為
項和為![]() ,試研究:是否存在實數
,試研究:是否存在實數![]() ,使得
,使得![]() 成等比數列(
成等比數列(![]() )?若存在,請求出
)?若存在,請求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(Ⅰ)![]() (Ⅱ)① 當
(Ⅱ)① 當![]() 為偶數時,
為偶數時,![]() ,
,
當![]() 為奇數時,
為奇數時,![]() ;②
;②![]()
【解析】
試題(Ⅰ)由新定義知:前![]() 項之和為兩等差數列之和,一個是首項為3,公差為8的等差數列前8項和,另一個是首項為17,公差為8的等差數列前7項和,所以前
項之和為兩等差數列之和,一個是首項為3,公差為8的等差數列前8項和,另一個是首項為17,公差為8的等差數列前7項和,所以前![]() 項之和
項之和![]() (Ⅱ)①根據新定義知:證明目標為
(Ⅱ)①根據新定義知:證明目標為![]() ,
,![]()
![]() ,相減得
,相減得![]() ,當
,當![]() 為奇數時,依次構成首項為a,公差為2的等差數列,
為奇數時,依次構成首項為a,公差為2的等差數列,![]() , 當
, 當![]() 為偶數時,依次構成首項為2-a,公差為2的等差數列,
為偶數時,依次構成首項為2-a,公差為2的等差數列,![]() ②先求和:當
②先求和:當![]() 為偶數時,
為偶數時, ;當
;當![]() 為奇數時,
為奇數時,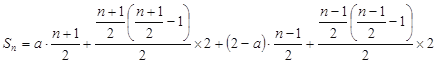
![]() 故當
故當![]() 時,
時,![]() ,
,![]() ,
,![]() , 由
, 由![]() ,則
,則![]() ,解得
,解得![]() .
.
試題解析:(Ⅰ)易得數列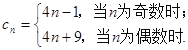
前![]() 項之和
項之和![]()
(Ⅱ)①![]() (
(![]() )(A)
)(A)
![]() (B)
(B)
(B)![]() (A)得
(A)得![]() (
(![]() ).
).
所以,![]() 為公差為2的“隔項等差”數列.
為公差為2的“隔項等差”數列.
當![]() 為偶數時,
為偶數時,![]() ,
,
當![]() 為奇數時,
為奇數時,![]() ;
;
②當![]() 為偶數時,
為偶數時,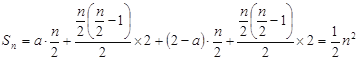 ;
;
當![]() 為奇數時,
為奇數時,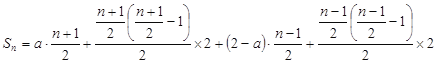
![]() .
.
故當![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,
由![]() ,則
,則![]() ,解得
,解得![]() .
.
所以存在實數![]() ,使得
,使得![]() 成等比數列(
成等比數列(![]() )
)


 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某校甲、乙、丙三個年級的學生志愿者人數分別是240,160,160.現采用分層抽樣的方法從中抽取7名同學去某敬老院參加獻愛心活動。
(1)應從甲、乙、丙三個年級的學生志愿者中分別抽取多少人?
(2)設抽出的7名同學分別用A,B,C,D,E,F,G表示,現從中隨機抽取2名同學承擔敬老院的衛生工作,求事件M“抽取的2名同學來自同一年級”發生的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的圓心在原點,半徑為
的圓心在原點,半徑為![]() ,若圓
,若圓![]() 與坐標軸的交點為頂點的四邊形是一個面積為
與坐標軸的交點為頂點的四邊形是一個面積為![]() 的正方形(記為
的正方形(記為![]() )設點
)設點![]() 在
在![]() 軸的負半軸上,以點
軸的負半軸上,以點![]() 、
、![]() 和點
和點![]() 為頂點的三角形的面積為
為頂點的三角形的面積為![]() .
.
(1)求圓![]() 的半徑
的半徑![]() 及點
及點![]() 的坐標;
的坐標;
(2)若過點![]() 的直線
的直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,當線段
兩點,當線段![]() 的中點落在正方形
的中點落在正方形![]() 內(包括邊界)時,求直線
內(包括邊界)時,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近期,某公交公司分別推出支付寶和徽信掃碼支付乘車活動,活動設置了一段時間的推廣期,由于推廣期內優惠力度較大,吸引越來越多的人開始使用掃碼支付.某線路公交車隊統計了活動剛推出一周內每一天使用掃碼支付的人次,用x表示活動推出的天數,y表示每天使用掃碼支付的人次(單位:十人次),統計數據如表l所示:
表1

根據以上數據,繪制了如右圖所示的散點圖.
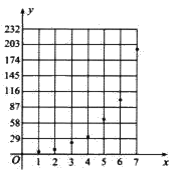
(1)根據散點圖判斷,在推廣期內,![]() (c,d均為大于零的常數)哪一個適宜作為掃碼支付的人次y關于活動推出天數x的回歸方程類型?(給出判斷即可,不必說明理由);
(c,d均為大于零的常數)哪一個適宜作為掃碼支付的人次y關于活動推出天數x的回歸方程類型?(給出判斷即可,不必說明理由);
(2)根據(1)的判斷結果及表1中的數據,求y關于x的回歸方程,并預測活動推出第8天使用掃碼支付的人次;
參考數據:

其中![]()
參考公式:
對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為: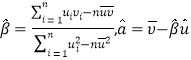 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】湖南省第九屆少數民族傳統體育運動會于2018年10月16日至20日在湘西龍山舉行.運動會期間,湖南省14個市州和17個民族縣市區組成的31個代表團2631人參加,來自土家、苗、瑤、侗、白、維吾爾、壯、回、漢等22個民族的1991名運動員分別參加陀螺、射弩、秋千、高腳、板鞋、蹴球、鍵球、押加、民族健身操及表演項目比賽,是湖南省歷屆民族運動會規模最大、規格最高、參賽人數最多的一次.對本次運動會中320名志愿者的年齡抽樣調查統計后得到樣本頻率分布直方圖(如圖),但是年齡組為![]() 的數據不慎丟失,請完成下面的解答.
的數據不慎丟失,請完成下面的解答.

(1)將頻率分布直方圖補充完整;
(2)估計本次省民運會中志愿者年齡的眾數和中位數(結果保留兩位小數);
(3)已知樣本容量為16,現在需要從樣本中30歲以下的志愿者中抽取2名志愿者談對本次運動會的感想,求被抽中的志愿者中恰有一名志愿者年齡不小于25歲的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校學生會為了解高二年級600名學生課余時間參加中華傳統文化活動的情況(每名學生最多參加7場).隨機抽取50名學生進行調查,將數據分組整理后,列表如下:
參加場數 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
占調查人數的百分比 | 8% | 10% | 20% | 26% | 18% | m% | 4% | 2% |
則以下四個結論中正確的是( )
A.表中m的數值為10
B.估計該年級參加中華傳統文化活動場數不高于2場的學生約為108人
C.估計該年級參加中華傳統文化活動場數不低于4場的學生約為216人
D.若采用系統抽樣方法進行調查,從該校高二600名學生中抽取容量為30的樣本,則分段間隔為15
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某地三角工廠分別位于邊長為2的正方形![]() 的兩個頂點
的兩個頂點![]() 及
及![]() 中點
中點![]() 處.為處理這三角工廠的污水,在該正方形區域內(含邊界)與
處.為處理這三角工廠的污水,在該正方形區域內(含邊界)與![]() 等距的點
等距的點![]() 處建一個污水處理廠,并鋪設三條排污管道
處建一個污水處理廠,并鋪設三條排污管道![]() ,記輔設管道總長為
,記輔設管道總長為![]() 千米.
千米.
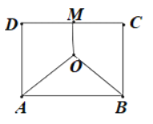
(1)按下列要求建立函數關系式:
(i)設![]() ,將
,將![]() 表示成
表示成![]() 的函數;
的函數;
(ii)設![]() ,將
,將![]() 表示成
表示成![]() 的函數;
的函數;
(2)請你選用一個函數關系,確定污水廠位置,使鋪設管道總長最短.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com