
【題目】已知圓![]() 的圓心在原點,半徑為
的圓心在原點,半徑為![]() ,若圓
,若圓![]() 與坐標軸的交點為頂點的四邊形是一個面積為
與坐標軸的交點為頂點的四邊形是一個面積為![]() 的正方形(記為
的正方形(記為![]() )設點
)設點![]() 在
在![]() 軸的負半軸上,以點
軸的負半軸上,以點![]() 、
、![]() 和點
和點![]() 為頂點的三角形的面積為
為頂點的三角形的面積為![]() .
.
(1)求圓![]() 的半徑
的半徑![]() 及點
及點![]() 的坐標;
的坐標;
(2)若過點![]() 的直線
的直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,當線段
兩點,當線段![]() 的中點落在正方形
的中點落在正方形![]() 內(包括邊界)時,求直線
內(包括邊界)時,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
【答案】(1)圓![]() 的方程為:
的方程為:![]() ,
, ![]() ,
,![]() ;(2)
;(2) 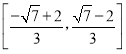
【解析】
(1)由圓![]() 與坐標軸的交點為頂點的四邊形是一個面積為
與坐標軸的交點為頂點的四邊形是一個面積為![]() ,求得
,求得![]() ,即可求得圓
,即可求得圓![]() 的方程
的方程
設點![]() 由
由![]() ,
,![]() ,以點
,以點![]() 、
、![]() 和點
和點![]() 為頂點的三角形的面積為
為頂點的三角形的面積為![]() ,即可得出
,即可得出![]() 到直線
到直線![]() 的距離為
的距離為![]() .即可求得
.即可求得![]() .
.
(2)設出直線的方程,將直線的方程與圓方程聯立,利用二次方程的韋達定理得到弦中點的坐標,根據中點在正方形的內部,得到中點的坐標滿足的不等關系,求出![]() 的范圍.
的范圍.
(1)![]() 圓
圓![]() 與坐標軸的交點為頂點的四邊形是一個面積為
與坐標軸的交點為頂點的四邊形是一個面積為![]()
![]() ,圓
,圓![]() 的方程為:
的方程為:![]() .
.
設點![]() ,
,![]() ,
,![]() ,以點
,以點![]() 、
、![]() 和點
和點![]() 為頂點的三角形的面積為
為頂點的三角形的面積為![]() ,得出
,得出![]() 到直線
到直線![]() 的距離為
的距離為![]() .則
.則![]() ,求得
,求得![]() (舍)或
(舍)或![]() ,
,![]()
![]() .
.
所以:圓![]() 的方程為:
的方程為:![]() ,
, ![]() ,
,![]() .
.
(2) 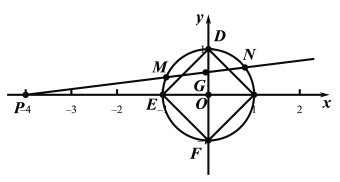
如圖,設![]() 的坐標分別為
的坐標分別為![]() ,
,![]() ,線段
,線段![]() 的中點為
的中點為![]() ,由
,由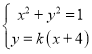 得:
得:![]() ,
,
由![]()
解得:![]() .
.
因為![]() ,
,![]() ,
,![]() ,
,
因為![]() ,所以
,所以![]() 不可能在
不可能在![]() 軸右邊,又直線
軸右邊,又直線![]() ,
,![]() ,當
,當![]() 落在正方形內(包括邊界)時,則有
落在正方形內(包括邊界)時,則有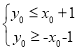 ,
,
即 化簡得:
化簡得: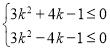 ,
,
解得:![]() .
.
直線![]() 的斜率的取值范圍
的斜率的取值范圍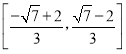


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,過橢圓
中,過橢圓![]() 右頂點
右頂點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于另外一點
于另外一點![]() ,已知點
,已知點![]() 的縱坐標為
的縱坐標為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點
兩點![]() 分別在直線
分別在直線![]() 的上、下方,設四邊形
的上、下方,設四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十七世紀法國數學家費馬提出猜想:“當整數![]() 時,關于
時,關于![]() 的方程
的方程![]() 沒有正整數解”.經歷三百多年,于二十世紀九十年中期由英國數學家安德魯
沒有正整數解”.經歷三百多年,于二十世紀九十年中期由英國數學家安德魯![]() 懷爾斯證明了費馬猜想,使它終成費馬大定理,則下面說法正確的是( )
懷爾斯證明了費馬猜想,使它終成費馬大定理,則下面說法正確的是( )
A. 存在至少一組正整數組![]() 使方程
使方程![]() 有解
有解
B. 關于![]() 的方程
的方程![]() 有正有理數解
有正有理數解
C. 關于![]() 的方程
的方程![]() 沒有正有理數解
沒有正有理數解
D. 當整數![]() 時,關于
時,關于![]() 的方程
的方程![]() 沒有正實數解
沒有正實數解
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)求證:數列![]() 是等差數列,求數列
是等差數列,求數列![]() 的通項公式;
的通項公式;
(3)若![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一直徑為8米的半圓形空地,現計劃種植甲、乙兩種水果,已知單位面積種植甲水果的經濟價值是種植乙水果經濟價值的5倍,但種植甲水果需要有輔助光照.半圓周上的![]() 處恰有一可旋轉光源滿足甲水果生長的需要,該光源照射范圍是
處恰有一可旋轉光源滿足甲水果生長的需要,該光源照射范圍是![]() ,點
,點![]() 在直徑
在直徑![]() 上,且
上,且![]() .
.

(1)若![]() 米,求
米,求![]() 的長;
的長;
(2)設![]() , 求該空地產生最大經濟價值時種植甲種水果的面積.
, 求該空地產生最大經濟價值時種植甲種水果的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列![]() 滿足:對于
滿足:對于![]() ,都有
,都有![]() (
(![]() 為常數),則稱數列
為常數),則稱數列![]() 是公差為
是公差為![]() 的“隔項等差”數列.
的“隔項等差”數列.
(Ⅰ)若![]() ,
,![]() 是公差為8的“隔項等差”數列,求
是公差為8的“隔項等差”數列,求![]() 的前
的前![]() 項之和;
項之和;
(Ⅱ)設數列![]() 滿足:
滿足:![]() ,對于
,對于![]() ,都有
,都有![]() .
.
①求證:數列![]() 為“隔項等差”數列,并求其通項公式;
為“隔項等差”數列,并求其通項公式;
②設數列![]() 的前
的前![]() 項和為
項和為![]() ,試研究:是否存在實數
,試研究:是否存在實數![]() ,使得
,使得![]() 成等比數列(
成等比數列(![]() )?若存在,請求出
)?若存在,請求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科室安排甲、乙、丙、丁四人國慶節放假期間(共放假八天)的值班表.已知甲、乙各值班四天,甲不能在第一天值班且甲、乙不在同一天值班;丙需要值班三天,且不能連續值班;丁需要值班五天;規定每天必須兩人值班.則符合條件的不同方案共有( )種.
A. 400 B. 700 C. 840 D. 960
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2-mlnx,h(x)=x2-x+a.
(1)當a=0時,f(x)≥h(x)在(1,+∞)上恒成立,求實數m的取值范圍;
(2)當m=2時,若函數k(x)=f(x)-h(x)在區間(1,3)上恰有兩個不同零點,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com