
| A. | A=4 | B. | ω=1 | C. | φ=$\frac{π}{6}$ | D. | B=4 |
分析 由函數的最值求出A、B,由周期求出ω,由五點法作圖求出φ的值,可得函數的解析式.
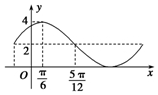
解答 解:根據函數f(x)=Asin(ωx+φ)+B,(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象,
可得A=4-2=2,B=2,$\frac{1}{4}$•T=$\frac{1}{4}•\frac{2π}{ω}$=$\frac{5π}{12}$-$\frac{π}{6}$=$\frac{π}{4}$,∴ω=2.
再根據五點法作圖可得2•$\frac{π}{6}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{6}$,
故選:C.
點評 本題主要考查利由函數y=Asin(ωx+φ)的部分圖象求解析式,由函數的最值求出A、B,由周期求出ω,由五點法作圖求出φ的值,屬于基礎題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向左平移$\frac{π}{8}$個單位 | B. | 向左平移$\frac{π}{4}$個單位 | ||
| C. | 向右平移$\frac{π}{8}$個單位 | D. | 向右平移$\frac{π}{4}$個單位 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
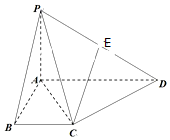 如圖,在四棱錐P-ABCD中,已知PA⊥平面ABCD,∠BAD=90°,AD∥BC,PA=AB=BC=1,AD=2,E為PD的中點.
如圖,在四棱錐P-ABCD中,已知PA⊥平面ABCD,∠BAD=90°,AD∥BC,PA=AB=BC=1,AD=2,E為PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 奇函數,在(-∞,0)上是減函數 | B. | 奇函數,在(-∞,0)上是增函數 | ||
| C. | 偶函數,在(-∞,0)上是減函數 | D. | 偶函數,在(-∞,0)上是增函數 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com