
【題目】
已知點![]() ,
,![]() ,動點P滿足
,動點P滿足![]() ,記動點P的軌跡為W.
,記動點P的軌跡為W.
(Ⅰ)求W的方程;
(Ⅱ)直線![]() 與曲線W交于不同的兩點C,D,若存在點
與曲線W交于不同的兩點C,D,若存在點![]() ,使得
,使得![]() 成立,求實數m的取值范圍.
成立,求實數m的取值范圍.
【答案】(Ⅰ)![]() . (Ⅱ)
. (Ⅱ)![]() .
.
【解析】
試題(Ⅰ)依題意,點P到兩定點A、B的距離之和為定值![]() ,且此值大于兩定點間的距離2,由橢圓定義可知動點P的軌跡是以A,B為焦點,長軸長為
,且此值大于兩定點間的距離2,由橢圓定義可知動點P的軌跡是以A,B為焦點,長軸長為![]() 的橢圓,從而寫出W的標準方程;
的橢圓,從而寫出W的標準方程;
(Ⅱ)先將直線方程與曲線W的方程聯立,得關于x的一元二次方程,利用韋達定理,寫出交點C、D的橫坐標的和與積,再求出線段CD的中垂線的方程,此直線與x軸的交點即為M,從而得m關于k的函數,求函數值域即可
試題解析:(Ⅰ)由橢圓的定義可知,動點P的軌跡是以A,B為焦點,長軸長為![]() 的橢圓.
的橢圓.
∴![]() ,
,![]() ,
,![]() .
.
W的方程是![]() .
.
(Ⅱ)設C,D兩點坐標分別為![]() 、
、![]() ,C,D中點為
,C,D中點為![]() .
.
由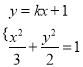 得
得![]() .
.
所以![]()
∴![]() , 從而
, 從而![]() .
.
∴![]() 斜率
斜率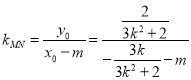 .
.
又∵![]() , ∴
, ∴![]() ,∴
,∴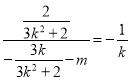 即
即![]()
當![]() 時,
時,![]() ;
;
當![]() 時,
時,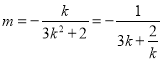
![]() .
.
故所求![]() 的取范圍是
的取范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】在極坐標系下,方程![]() 的圖形為如圖所示的“幸運四葉草”,又稱為玫瑰線.
的圖形為如圖所示的“幸運四葉草”,又稱為玫瑰線.
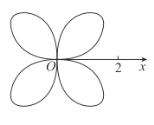
(1)當玫瑰線的![]() 時,求以極點為圓心的單位圓與玫瑰線的交點的極坐標;
時,求以極點為圓心的單位圓與玫瑰線的交點的極坐標;
(2)求曲線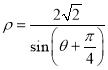 上的點M與玫瑰線上的點N距離的最小值及取得最小值時的點M、N的極坐標(不必寫詳細解題過程).
上的點M與玫瑰線上的點N距離的最小值及取得最小值時的點M、N的極坐標(不必寫詳細解題過程).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,以原點O為極點,x軸的正半軸為極軸建立極坐標系,已知直線l的參數方程為: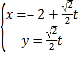 ,
,![]() 為參數
為參數![]() 點的極坐標為
點的極坐標為![]() ,曲線C的極坐標方程為
,曲線C的極坐標方程為![]() .
.
![]() Ⅰ
Ⅰ![]() 試將曲線C的極坐標方程化為直角坐標方程,并求曲線C的焦點在直角坐標系下的坐標;
試將曲線C的極坐標方程化為直角坐標方程,并求曲線C的焦點在直角坐標系下的坐標;
![]() Ⅱ
Ⅱ![]() 設直線l與曲線C相交于兩點A,B,點M為AB的中點,求
設直線l與曲線C相交于兩點A,B,點M為AB的中點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知橢圓![]() 上任意一點到其兩個焦點
上任意一點到其兩個焦點![]() ,
,![]() 的距離之和等于
的距離之和等于![]() ,焦距為2c,圓
,焦距為2c,圓![]() ,
,![]() ,
,![]() 是橢圓的左、右頂點,AB是圓O的任意一條直徑,四邊形
是橢圓的左、右頂點,AB是圓O的任意一條直徑,四邊形![]() 面積的最大值為
面積的最大值為![]() .
.
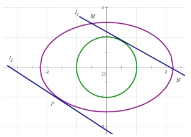
(1)求橢圓C的方程;
(2)如圖,若直線![]() 與圓O相切,且與橢圓相交于M,N兩點,直線
與圓O相切,且與橢圓相交于M,N兩點,直線![]() 與
與![]() 平行且與橢圓相切于P(O,P兩點位于
平行且與橢圓相切于P(O,P兩點位于![]() 的同側),求直線
的同側),求直線![]() ,
,![]() 距離d的取值范圍.
距離d的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市旅游局為了進一步開發旅游資源,需要了解游客的情況,以便制定相應的策略,在某月中隨機抽取甲、乙兩個景點各10天的游客數,畫出莖葉圖如下:若景點甲中的數據的中位數是126,景點乙中的數據的平均數是124.
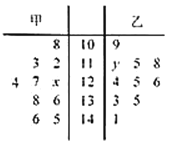
(1)求![]() ,
,![]() 的值;
的值;
(2)若將圖中景點甲中的數據作為該景點較長一段時期內的樣本數據(視樣本頻率為概率).今從這段時期內任取4天,記其中游客數不低于125人的天數為![]() ,求概率
,求概率![]() ;
;
(3)現從上圖的共20天的數據中任取2天的數據(甲、乙兩景點中各取1天),記其中游客數不低于115且不高于135人的天數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]() .
.

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,從參加環保知識競賽的學生中抽出![]() 名,將其成績(均為整數)整理后畫出的頻率分布直方圖如下:觀察圖形,回答下列問題:
名,將其成績(均為整數)整理后畫出的頻率分布直方圖如下:觀察圖形,回答下列問題:

(1)![]() 這一組的頻數、頻率分別是多少?
這一組的頻數、頻率分別是多少?
(2)估計這次環保知識競賽成績的平均數、眾數、中位數。(不要求寫過程)
(3) 從成績是80分以上(包括80分)的學生中選兩人,求他們在同一分數段的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com