
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]() .
.

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)根據題設條件可以得出AB⊥AP,CD⊥PD.而AB//CD,就可證明出AB⊥平面PAD.
進而證明出平面PAB⊥平面PAD.(2)先找出AD中點,找出相互垂直的線,建立以![]() 為坐標原點,
為坐標原點, ![]() 的方向為
的方向為![]() 軸正方向,
軸正方向, ![]() 為單位長的空間直角坐標系,列出所需要的點的坐標,設
為單位長的空間直角坐標系,列出所需要的點的坐標,設![]() 是平面
是平面![]() 的法向量,
的法向量, ![]() 是平面
是平面![]() 的法向量,根據垂直關系,求出
的法向量,根據垂直關系,求出![]() 和
和![]() ,利用數量積公式可求出二面角的平面角.
,利用數量積公式可求出二面角的平面角.
試題解析:(1)由已知![]() ,得AB⊥AP,CD⊥PD.
,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,從而AB⊥平面PAD.
又AB ![]() 平面PAB,所以平面PAB⊥平面PAD.
平面PAB,所以平面PAB⊥平面PAD.
(2)在平面![]() 內做
內做![]() ,垂足為
,垂足為![]() ,
,
由(1)可知, ![]() 平面
平面![]() ,故
,故![]() ,可得
,可得![]() 平面
平面![]() .
.
以![]() 為坐標原點,
為坐標原點, ![]() 的方向為
的方向為![]() 軸正方向,
軸正方向, ![]() 為單位長,建立如圖所示的空間直角坐標系
為單位長,建立如圖所示的空間直角坐標系![]() .
.
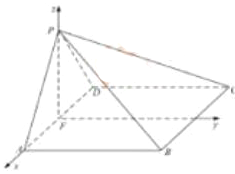
由(1)及已知可得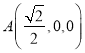 ,
, 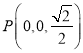 ,
, 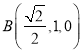 ,
,  .
.
所以 ,
, ![]() ,
,  ,
, ![]() .
.
設![]() 是平面
是平面![]() 的法向量,則
的法向量,則
![]() ,即
,即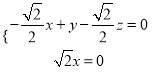 ,
,
可取![]() .
.
設![]() 是平面
是平面![]() 的法向量,則
的法向量,則
![]() ,即
,即 ,
,
可取![]() .
.
則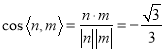 ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.
點睛:高考對空間向量與立體幾何的考查主要體現在以下幾個方面:①求異面直線所成的角,關鍵是轉化為兩直線的方向向量的夾角;②求直線與平面所成的角,關鍵是轉化為直線的方向向量和平面的法向量的夾角;③求二面角,關鍵是轉化為兩平面的法向量的夾角.建立空間直角坐標系和表示出所需點的坐標是解題的關鍵.


科目:高中數學 來源: 題型:
【題目】某校1200名高三年級學生參加了一次數學測驗(滿分為100分),為了分析這次數學測驗的成績,從這1200人的數學成績中隨機抽出200人的成績繪制成如下的統計表,請根據表中提供的信息解決下列問題;
(1)求a、b、c的值;
(2)如果從這1200名學生中隨機取一人,試估計這名學生該次數學測驗及格的概率p(注:60分及60分以上為及格);
(3)試估計這次數學測驗的年級平均分.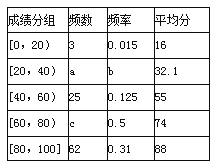
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0),四點P1(1,1),P2(0,1),P3(–1,
(a>b>0),四點P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三點在橢圓C上.
)中恰有三點在橢圓C上.
(1)求C的方程;
(2)設直線l不經過P2點且與C相交于A,B兩點.若直線P2A與直線P2B的斜率的和為–1,證明:l過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,已知△ABC的面積為![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,側棱垂直底面,∠ACB=90°,AC=BC= ![]() AA1 , D是棱AA1的中點.
AA1 , D是棱AA1的中點.
(Ⅰ)證明:平面BDC1⊥平面BDC
(Ⅱ)平面BDC1分此棱柱為兩部分,求這兩部分體積的比.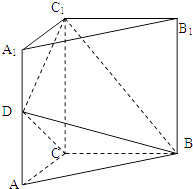
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,已知曲線![]() 的參數方程為
的參數方程為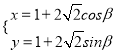 (
(![]() 為參數),在極坐標系中,直線
為參數),在極坐標系中,直線![]() 的方程為:
的方程為: ![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
(Ⅰ)寫出曲線![]() 的直角坐標方程,并指出它是何種曲線;
的直角坐標方程,并指出它是何種曲線;
(Ⅱ)設![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,
兩點, ![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,PA⊥底面ABC, ![]() .點D,E,N分別為棱PA,PC,BC的中點,M是線段AD的中點,PA=AC=4,AB=2.
.點D,E,N分別為棱PA,PC,BC的中點,M是線段AD的中點,PA=AC=4,AB=2.
(Ⅰ)求證:MN∥平面BDE;
(Ⅱ)求二面角C-EM-N的正弦值;
(Ⅲ)已知點H在棱PA上,且直線NH與直線BE所成角的余弦值為![]() ,求線段AH的長.
,求線段AH的長.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com