
分析 (1)求導,由f'(1)=-8,求得a的值,分別求得切線方程,與原切線方程比較,即可求得a的值;
(2)求導,根據導數與函數單調性的關系,分類討論,即可求得函數f(x)(x>0)的單調區間與極值;
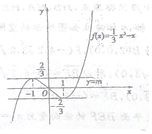
(3)由(2)可知:根據函數的單調性,求得f(x)的極值,分別作出函數$f(x)=\frac{1}{3}{x^3}-x$與y=m的圖象,從圖象上可以看出當$-\frac{2}{3}<m<\frac{2}{3}$時,兩個函數的圖象有三個不同的交點,即可求得m的取值范圍.
解答 解:(1)f'(x)=ax2+(1-a2)x-a,由8x+y-2=0可得f'(1)=-8,
即f'(1)=a+(1-a2)-a=-8,解得a=±3,
當a=3時,f(x)=x3-4x2-3x,f(1)=-6,f'(x)=3x2-8x-3,f'(1)=-8,
當a=-3時,f(x)=-x3-4x2+3,f(1)=-2,f'(x)=-3x2-8x+3,f'(1)=-8,
故曲線y=f(x)在點(1,f(1))處的切線方程為y+2=-8(x-1),即8x+y-6=0不符合題意,舍去,
故a的值為3.
(2)當a≠0時,f′(x)=ax2+(1-a2)x-a=(x-a)(ax+1)=a(x-a)(x+$\frac{1}{a}$),
當a>0時,令f'(x)=0,則${x_1}=-\frac{1}{a},{x_2}=a$
當x變化時,f'(x),f(x)的變化情況如下表:
| x | (-∞,-$\frac{1}{a}$) | -$\frac{1}{a}$ | (-$\frac{1}{a}$,a) | a | (a,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↑ | 極大值 | ↓ | 極小值 | ↑ |
| x | (-∞,a) | a | (a,-$\frac{1}{a}$) | -$\frac{1}{a}$ | (-$\frac{1}{a}$,+∞) |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | ↓ | 極小值 | ↑ | 極大值 | ↓ |
點評 本題考查導數的綜合應用,考查利用導數求函數的單調性區間及最值,考查方程解得個數,考查數形結合思想,考查計算能力,屬于難題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
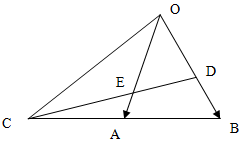 已知△ABO中,延長BA到C,使AC=BA,D是將$\overrightarrow{OB}$分成2:1的一個分點,DC和OA交于E,設$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$
已知△ABO中,延長BA到C,使AC=BA,D是將$\overrightarrow{OB}$分成2:1的一個分點,DC和OA交于E,設$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | N⊆M | B. | M⊆N | C. | N∩M={2} | D. | N∪M=R |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com