
【題目】已知等比數(shù)列![]() 的公比
的公比![]() ,前n項和為
,前n項和為![]() .若
.若![]() ,且
,且![]() 是
是![]() 與
與![]() 的等差中項.
的等差中項.
(1)求![]() ;
;
(2)數(shù)列![]() 滿足
滿足![]() ,
,![]() ,求數(shù)列
,求數(shù)列![]() 的前2019項和;
的前2019項和;
(3)設(shè)![]() ,問數(shù)列
,問數(shù)列![]() 中是否存在三項,它們可以構(gòu)成等差數(shù)列?若存在,請求出一組適合條件的項;若不存在,請說明理由.
中是否存在三項,它們可以構(gòu)成等差數(shù)列?若存在,請求出一組適合條件的項;若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)不存在,理由見解析
;(3)不存在,理由見解析
【解析】
(1)結(jié)合等差中項的性質(zhì),將已知條件轉(zhuǎn)化為![]() 的形式,由此求得
的形式,由此求得![]() ,進而求得
,進而求得![]() .
.
(2)利用分組求和法求得數(shù)列![]() 的前
的前![]() 項和.
項和.
(3)存在![]() ,且
,且![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差數(shù)列,根據(jù)等差中項的性質(zhì)列方程,化簡后推出矛盾,由此判斷出不存在符合條件的項.
成等差數(shù)列,根據(jù)等差中項的性質(zhì)列方程,化簡后推出矛盾,由此判斷出不存在符合條件的項.
(1)由![]() ,得
,得![]() ①.
①.
再由![]() 是
是![]() ,
,![]() 的等差中項,得
的等差中項,得![]() ,
,
即![]() ②.
②.
由①②,得![]() ,
,
即![]() ,亦即
,亦即![]() ,
,
解得![]() 或
或![]() ,又
,又![]() ,故
,故![]() .
.
代入①,得![]() ,
,
所以![]() ,
,
即![]() ;
;
(2)![]()
![]()
![]()
(3)設(shè)存在![]() ,且
,且![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差數(shù)列,
成等差數(shù)列,
∴![]()
即![]()
∴![]()
∴![]() (*)
(*)
因為![]() 且
且![]()
∴![]() 、
、![]() 為偶數(shù)
為偶數(shù)
![]() 為奇數(shù),(*)式產(chǎn)生矛盾.所以這樣的三項不存在.
為奇數(shù),(*)式產(chǎn)生矛盾.所以這樣的三項不存在.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】在5件產(chǎn)品中,有3件一等品和2件二等品,從中任取2件,以![]() 為概率的事件是( )
為概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的長軸長是短軸長的
的長軸長是短軸長的![]() 倍,且過點
倍,且過點![]() .
.
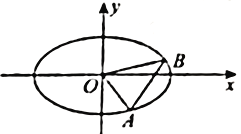
(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)若![]() 的頂點
的頂點![]() 、
、![]() 在橢圓上,
在橢圓上, ![]() 所在的直線斜率為
所在的直線斜率為![]() ,
, ![]() 所在的直線斜率為
所在的直線斜率為![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)設(shè)![]() ,試討論
,試討論![]() 單調(diào)性;
單調(diào)性;
(2)設(shè)![]() ,當(dāng)
,當(dāng)![]() 時,任意
時,任意![]() ,存在
,存在![]() ,使
,使![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知動圓過定點![]() ,且在
,且在![]() 軸上截得線段
軸上截得線段![]() 的長為 4,直線
的長為 4,直線![]() 交
交![]() 軸于點
軸于點![]() .
.
(1)求動圓圓心的軌跡![]() 的方程;
的方程;
(2)直線![]() 與軌跡
與軌跡![]() 交于
交于![]() 兩點,分別以
兩點,分別以![]() 為切點作軌跡
為切點作軌跡![]() 的切線交于點
的切線交于點![]() ,若
,若![]() .試判斷實數(shù)
.試判斷實數(shù)![]() 所滿足的條件,并說明理由.
所滿足的條件,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
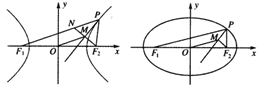
【題目】如圖,P是雙曲線![]() (a>0,b>0,xy≠0)上的動點,F(xiàn)1,F(xiàn)2是雙曲線的焦點,M是∠F1PF2的平分線上一點,且
(a>0,b>0,xy≠0)上的動點,F(xiàn)1,F(xiàn)2是雙曲線的焦點,M是∠F1PF2的平分線上一點,且![]() .某同學(xué)用以下方法研究|OM|:延長F2M交PF1于點N,可知△PNF2為等腰三角形,且M為F2N的中點,得|OM|=
.某同學(xué)用以下方法研究|OM|:延長F2M交PF1于點N,可知△PNF2為等腰三角形,且M為F2N的中點,得|OM|=![]() |NF1|=…=a。類似地:P是橢圓
|NF1|=…=a。類似地:P是橢圓![]() (a>b>0,xy≠0)上的動點,F(xiàn)1,F(xiàn)2是橢圓的焦點,M是∠F1PF2的平分線上一點,且
(a>b>0,xy≠0)上的動點,F(xiàn)1,F(xiàn)2是橢圓的焦點,M是∠F1PF2的平分線上一點,且![]() ,則|OM|的取值范圍是________.
,則|OM|的取值范圍是________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的兩焦點與短軸的一個端點的連線構(gòu)成等腰直角三角形,
的兩焦點與短軸的一個端點的連線構(gòu)成等腰直角三角形,
直線![]() 與以橢圓C的右焦點為圓心,以橢圓的長半軸長為半徑的圓相切.
與以橢圓C的右焦點為圓心,以橢圓的長半軸長為半徑的圓相切.
(Ⅰ)求橢圓C的方程;
(Ⅱ)設(shè)P為橢圓C上一點,若過點![]() 的直線
的直線![]() 與橢圓C相交于不同的兩點S和T,
與橢圓C相交于不同的兩點S和T,
滿足![]() (O為坐標(biāo)原點),求實數(shù)
(O為坐標(biāo)原點),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了讓學(xué)生了解環(huán)保知識,增強環(huán)保意識,某中學(xué)舉行了一次“環(huán)保知識競賽”,共有900名學(xué)生參加了這次競賽.為了解本次競賽成績情況,從中抽取了部分學(xué)生的成績(得分均為整數(shù),滿分為100分)進行統(tǒng)計.請你根據(jù)尚未完成并有局部污損的頻率分布表和頻數(shù)分布直方圖,解答下列問題:
分組 | 頻數(shù) | 頻率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 10 | |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合計 | 50 |
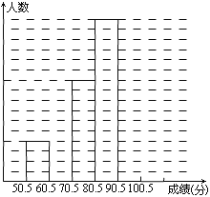
(Ⅰ)填充頻率分布表的空格(將答案直接填在表格內(nèi));
(Ⅱ)補全頻數(shù)條形圖;
(Ⅲ)若成績在75.5~85.5分的學(xué)生為二等獎,問獲得二等獎的學(xué)生約為多少人?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】編號分別為![]() 的16名籃球運動員在某次訓(xùn)練比賽中的得分記錄如下:
的16名籃球運動員在某次訓(xùn)練比賽中的得分記錄如下:
運動員編號 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
運動員編號 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(1)將得分在對應(yīng)區(qū)間內(nèi)的人數(shù)填入相應(yīng)的空格:
區(qū)間 | [10,20) | [20,30) | [30,40] |
人數(shù) |
(2)從得分在區(qū)間[20,30)內(nèi)的運動員中隨機抽取2人.
(ⅰ)用運動員編號列出所有可能的抽取結(jié)果;
(ⅱ)求這2人得分之和大于50的概率.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com