Question

【題目】將長為、寬為的矩形劃分為個小正方形.一粒子不重復不遺漏連續地通過每個小正方形的一條對角線.這件事能否辦到？若辦不到，請說明理由；若能辦到，請給出一種行走路線.

Answer 1

【答案】能

【解析】

能辦到.

分兩種情況說明：

（1）

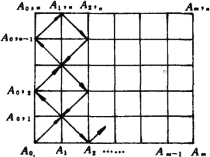
若、中至少有一個是奇數，不妨設為奇數.如圖，粒子從開始行走，至；；；；；.即給出時粒子的一種行走路線.若，則粒子可繼續從出發，行至；；；；.又給出時粒子的一種行走路線.假設時粒子已有，時的一種行走路線，那么，當時，若為奇數，粒子在長為，寬為的矩形上的個小正方形的一種行走路線終止于處，再沿下述行走路線即可：；；；；；若為偶數，粒子在長為，寬為的矩形上的個小正方形的一種行走路線終止于，再沿下述行走路線即可：；；；；.至此，已給出時粒子的一種行走路線.

由數學歸納法原理，當時，均可設計出粒子的一種行走路線.

（2）

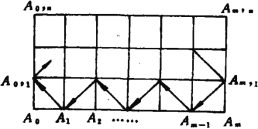
若、都是偶數，如圖，粒子從開始行走至，然后在線段上方長為、寬為的矩形的個小正方形中行走.由（1）可知粒子有一種行走路線，終止于.此粒子再沿以下路線行走即可：；；；；；；.